题目内容
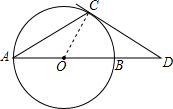
如图,已知AB是⊙O的直径,AB=2,∠BAC=30°,点C在⊙O上,过点C与⊙O相切的直线交AB的延长线于点D,求线段BD的长.


连接OC;
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠COD=∠A+∠OCA=60°;
∵CD切⊙O于C,
∴∠OCD=90°,
∴∠D=90°-60°=30°;
∵直径AB=2,
∴⊙O的半径OC=OB=1,
∴OD=2CO=2;
又∵OB=1,
∴BD=OD-OB=1.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠COD=∠A+∠OCA=60°;
∵CD切⊙O于C,
∴∠OCD=90°,
∴∠D=90°-60°=30°;
∵直径AB=2,
∴⊙O的半径OC=OB=1,
∴OD=2CO=2;
又∵OB=1,
∴BD=OD-OB=1.


练习册系列答案
相关题目








