题目内容
【题目】如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=![]() .
.
(1)求抛物线的对称轴和点P的坐标.
(2)在抛物线的对称轴上是否存在这样的点D,使△ABD为直角三角形?如果存在,求点D的坐标;如果不存在,请说明理由.
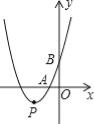
【答案】(1)对称轴是直线x=-2,P点坐标为(﹣2,﹣1);(2)存在,D1(﹣2,![]() ),D2(﹣2,2),D3(﹣2,1);D4(﹣2,
),D2(﹣2,2),D3(﹣2,1);D4(﹣2,![]() ).
).
【解析】
试题分析:(1)根据自变量与函数值的对应关系,可得B点坐标,根据正切函数,可得A点坐标,根据待定系数法,可得函数解析式,根据配方法,可得抛物线的对称轴和顶点坐标;(2)根据勾股定理,可得AD2=1+m2,AB2=12+32=10,BD2=4+(m﹣3)2,根据勾股定理的逆定理,可得关于m的方程,根据解方程,可得答案.
试题解析:(1)当x=0时,y=3,即B(0,3).tan∠ABO=![]() =
=![]() =
=![]() ,AO=1,即A点坐标为(﹣1,3).将A点坐标代入,得1﹣b+3=0,解得b=4.抛物线的解析式为y=x2+4x+3,y=(x+2)2﹣1,即P点坐标为(﹣2,﹣1);(2)在抛物线的对称轴上存在这样的点D,使△ABD为直角三角形.设D点坐标为D(﹣2,m),因为A(﹣1,0),B(0,3).由勾股定理,得AD2=1+m2,AB2=12+32=10,BD2=4+(m﹣3)2.①当AD2+AB2=BD2时,即1+m2+10=4+(m﹣3)2,解得m=
,AO=1,即A点坐标为(﹣1,3).将A点坐标代入,得1﹣b+3=0,解得b=4.抛物线的解析式为y=x2+4x+3,y=(x+2)2﹣1,即P点坐标为(﹣2,﹣1);(2)在抛物线的对称轴上存在这样的点D,使△ABD为直角三角形.设D点坐标为D(﹣2,m),因为A(﹣1,0),B(0,3).由勾股定理,得AD2=1+m2,AB2=12+32=10,BD2=4+(m﹣3)2.①当AD2+AB2=BD2时,即1+m2+10=4+(m﹣3)2,解得m=![]() ,即D1(﹣2,
,即D1(﹣2,![]() );②当AD2+BD2=AB2时,即1+m2+4+(m﹣3)2=10,解得m=2或m=1,即D2(﹣2,2),D3(﹣2,1);③当AB2+BD2=AD2时,即10+4+(m﹣3)2=1+m2,解得m=
);②当AD2+BD2=AB2时,即1+m2+4+(m﹣3)2=10,解得m=2或m=1,即D2(﹣2,2),D3(﹣2,1);③当AB2+BD2=AD2时,即10+4+(m﹣3)2=1+m2,解得m=![]() ,即D4(﹣2,
,即D4(﹣2,![]() ),综上所述:在抛物线的对称轴上存在这样的点D,使△ABD为直角三角形.其坐标为D1(﹣2,
),综上所述:在抛物线的对称轴上存在这样的点D,使△ABD为直角三角形.其坐标为D1(﹣2,![]() ),D2(﹣2,2),D3(﹣2,1);D4(﹣2,
),D2(﹣2,2),D3(﹣2,1);D4(﹣2,![]() ).
).

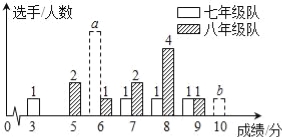
【题目】2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m= ,n= ;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.