题目内容
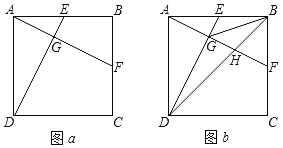
【题目】如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.
(1)求证:AF⊥DE;
(2)如图b,连接BG,BD,BD交AF于点H.
①求证:GB2=GAGD;
②若AB=10,求三角形GBH的面积.
【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】
(1)利用正方形性质结合题意得出AE=BF,由此进一步证明△ADE与△BAF全等,从而得出∠BAF=∠ADE,再进一步通过等量代换求得∠ADE+∠DAF=90°,据此进一步分析即可证明结论;
(2)①首先证明△ABN△DAG得出AG=BN,DG=AN,然后再根据EG∥BN得出![]() ,所以AG=GN,最后利用勾股定理可知在Rt△BNG中BG2=BN2+GN2,由此通过等量代换进一步证明结论即可;②首先通过勾股定理求出DE,然后利用三角形等面积法求出AG,从而得知GN与BN,进一步利用△DGH~△BNH得出GH=2HN,然后结合题意计算出GH,最后进一步计算答案即可.
,所以AG=GN,最后利用勾股定理可知在Rt△BNG中BG2=BN2+GN2,由此通过等量代换进一步证明结论即可;②首先通过勾股定理求出DE,然后利用三角形等面积法求出AG,从而得知GN与BN,进一步利用△DGH~△BNH得出GH=2HN,然后结合题意计算出GH,最后进一步计算答案即可.
(1)∵正方形ABCD,E、F分别为边AB、BC的中点,
∴AD=BC=DC=AB,AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,
BC,
∴AE=BF,
∵在△ADE和△BAF中,
∵
∴△ADE△BAF(SAS)
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=90°,
∴∠ADE+∠DAF=90°,
∴∠AGD=90°,
∴AF⊥DE;
(2)①如图b,过点B作BN⊥AF于N,
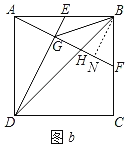
由(1)可得:∠BAF=∠ADE,∠AGD=90°,AB=AD,
∴在△ABN与△DAG中,∠AGD=∠ANB=90°,∠BAF=∠ADE,AB=AD,
∴△ABN△DAG(AAS)
∴AG=BN,DG=AN,
∵∠AGE=∠ANB=90°,
∴EG∥BN,
∴![]() ,且AE=BE,
,且AE=BE,
∴AG=GN,
∴AN=2AG=DG,
∵在Rt△BNG中,BG2=BN2+GN2,
∴BG2=AG2+AG2,
∴GB2=2AG2=2AGAG=GAGD,
即:GB2=GAGD;
②∵AB=10,
∴AE=BF=5,
∴DE=![]() =
=![]() =5
=5![]() ,
,
∵![]() ×AD×AE=
×AD×AE=![]() ×DE×AG,
×DE×AG,
∴AG=2![]() ,
,
∴AG=GN=BN=2![]() ,
,
∴AN=DG=4![]() ,
,
∵GE∥BN,
∴△DGH~△BNH,
∴![]() =
=![]() =2,
=2,
∴GH=2HN,
∵GH+HN=GN=2![]() ,
,
∴GH=![]() ,
,
∴△GBH的面积=![]() ×GH×BN=
×GH×BN=![]() ×
×![]() ×2
×2![]() =
=![]() .
.

【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
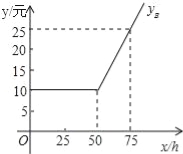
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
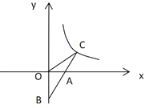
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
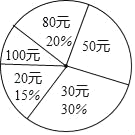
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.
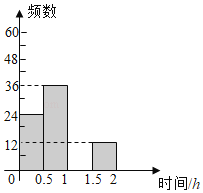
【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.