题目内容
【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为![]() .
.

(1)图①中打包带的总长![]() =________.
=________.
图②中打包带的总长![]() =________.
=________.
(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较 ![]() 的大小.)
的大小.)
(3)若b=40且a为正整数,在数轴上表示数![]() 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
【答案】(1)l=4a+2b+180,l=2a+4b+180;(2)第2种,l- l=2(a-b),理由见解析;
(3)a=50
【解析】
(1)根据图形,不难看出:图①打包带的长有长方体的四个长、两个宽、六个高,图②打包带的长有长方体的两个长、四个宽、六个高,从而可以解答本题;
(2)根据(1)中的答案可以求得哪一种打包方式更节省材料;
(3)根据(2)中的关系式,代入b的值,再根据![]() 的两点之间有且只有19个整数点即可求解.
的两点之间有且只有19个整数点即可求解.
解:(1)图①四个长为4a,两个宽为2b,六个高为30×6=180,
∴打包带的长l=4a+2b+180,
图②两个长为2a,四个宽为4b,六个高为30×6=180,
∴打包带的长l=2a+4b+180,
故答案为l=4a+2b+180,l=2a+4b+180.
(2)第2种打包方式更节省材料,理由如下:
(4a+2b+180)-(2a+4b+180),
=4a+2b+180-2a-4b-180,
=2(a-b),
∵![]() ,
,
∴2(a-b)>0,
∴第2种打包方式更节省材料;
(3)当![]() 时, 2(a-b)=2(a-40) =2a-80,
时, 2(a-b)=2(a-40) =2a-80,
∵在数轴上表示数![]() 的两点之间有且只有19个整数点, 且
的两点之间有且只有19个整数点, 且![]() 为正整数,
为正整数,
∴a=50.

【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: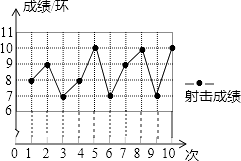
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.
【题目】近几年某市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出不完整的统计表如下:
升学意向 | 省级示范高中 | 市级示范高中 | 一般高中 | 职业高中 | 其他 | 合计 |
人数 | 15 | 15 | 9 | 3 | m | |
百分比 | 25% | 25% | n | 5% | 100% |
请你根据统计表提供的信息解答下列问题:
(1)表中m的值为 ,n的值为 ;
(2)补全图7中的条形统计图;
(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?


