题目内容
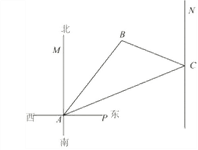
【题目】某海船以
海里/小时的速度向北偏东70°方向行驶，在A处看见灯塔B在海船的北偏东40°方向，5小时后船行驶到C处，发现此时灯塔B在海船的北偏西65°方向，求此时灯塔B到C处的距离。
【答案】BC=10
（海里）
【解析】试题分析：
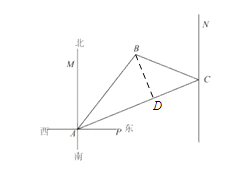
过点B作BD⊥AC于点D，将△ABC分成两个特殊的直角三角形，一个是等腰直角三角形，一个是含30°角的直角三角形，结合勾股定理列方程求解.
试题解析：
过点B作BD⊥AC于点D.
因为∠MAB=40°，∠MAC=70°，所以∠BAC=70°-40°=30°，
又因为∠NCB=65°，∠NCA=180°-70°=110°，所以∠ACB=45°，
所以DB=CD，AD=
.
设CD=x，则BD=x，AD=
.
所以+x=5×
，解得x=10.
所以BC=
.
此时灯塔B到C处的距离是海里.
练习册系列答案
相关题目
