题目内容
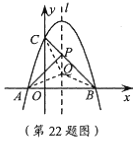
【题目】如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。

【答案】(1)m=2,(1,4);(2)(1,2).
【解析】
试题分析:(1)把点B的坐标为(3,0)代入![]() ,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
,解方程即可得m的值,求出m的值后把抛物线化为顶点式即可得抛物线的顶点坐标;(2)连接BC交抛物线的对称轴于点P,此时PA+PC的值最小,利用待定系数法求得直线BC的解析式,再求点P的坐标即可.
试题解析:(1)把点B的坐标为(3,0)代入得:![]() ,
,
解得m=2,
∴![]()
∵![]()
∴顶点坐标为(1,4).
(2)连接BC交抛物线的对称轴l于点P,此时PA+PC的值最小,
设Q是直线l上任意一点,连结AQ,CQ,BQ,
∵直线L垂直平分AB,
∴AQ=BQ,AP=BP,
∴AQ+CQ=BQ+CQ≥BC,
BC=BP+CP=AP+CP,
即AQ+CQ≥AP+CP
设直线BC的解析式为y=kx+b(k≠0),
把(3,0),(0,3)代入得,
![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=-x+3,
当x=1时,y=-1+3=2.
答:当PA+PC的值最小时,点P的坐标为(1,2).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


