题目内容
已知反比例函数 经过点A(x1,y1)、B(x2,y2),如果x1<x2<0,那么y1与y2的大小关系是
经过点A(x1,y1)、B(x2,y2),如果x1<x2<0,那么y1与y2的大小关系是
- A.y1>y2>0
- B.y2>y1>0
- C.y2<y1<0
- D.y1<y2<0
C
分析:先根据k=2>0、0>x2>x1判断出反比例函数所在的象限,再根据反比例函数的性质判断出y1、y2的大小.
解答:因为k=2>0.
所以图象分别位于第一、三象限,
又因为在每个象限内y随x的增大而减小,
当x1<x2<0时,对应点分布在第三象限,
故0>y1>y2,
故选:C.
点评:本题考查了反比例函数图象上点的性质,由反比例函数图象的性质判断函数图象上点的坐标特征,同学们应重点掌握.
分析:先根据k=2>0、0>x2>x1判断出反比例函数所在的象限,再根据反比例函数的性质判断出y1、y2的大小.
解答:因为k=2>0.
所以图象分别位于第一、三象限,
又因为在每个象限内y随x的增大而减小,
当x1<x2<0时,对应点分布在第三象限,
故0>y1>y2,
故选:C.
点评:本题考查了反比例函数图象上点的性质,由反比例函数图象的性质判断函数图象上点的坐标特征,同学们应重点掌握.

练习册系列答案
相关题目
 经过点B(1,1) .
经过点B(1,1) . ,写出
,写出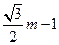 )(其中m>0),在线段OF上任取一点E,
)(其中m>0),在线段OF上任取一点E,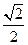 ,求代数式
,求代数式 的值.
的值.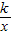 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 .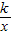 经过点A(-2,3),则其函数表达式为 .
经过点A(-2,3),则其函数表达式为 .