Question

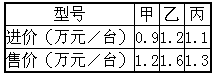
“5·12”汶川大地震后，某健身器材销售公司通过当地“红十字会”向灾区献爱心，捐出了五月份全部销售利润，已知该公司五月份只售出甲、乙、丙三种型号器材若干台，每种型号器材不少于8台，五月份支出包括这批器材进货款64万元和其他各项支出（含人员工资和杂项开支）3.8万元，这三种器材的进价和售价如下表，人员工资y₁（万元）和杂项支出y₂（万元）分别与总销售量x（台）成一次函数关系（如图所示）。

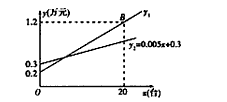
（1）求y₁与x的函数解析式；
（2）求五月份该公司的总销售量；
（3）设公司五月份售出甲种型号器材t台，五月份总销售利润为W（万元），求W与t的函数关系式；（销售利润=销售额一进价一其他各项支出）
（4）请推测该公司这次向灾区捐款金额的最大值。

Answer 1

解：（1）设y₁=kx+b（k＞0），
则：b=0.2，20k+b=1.2，
解得：k=0.05，b=0.2，
∴y₁与x的函数关系式为y=0.05x+0.2；
（2）依题意得：y₁+y₂=0.05x+0.2+0.005x+0.3=3.8，
解得：x=60，
∴五月份该公司的总销售量为60台；
（3）设五月份售出乙种型号器材p台，则售出丙种型号器材（60-t-p）台，
0.9t+1.2p+1.1（60-t-p）=64，
解得p=2t-20，
∴W=1.2t+1.6（2t-20）+1.3（60-t-2t+20）-64-3.8，
即W与t的函数关系式为：W=0.5t+4.2；
（4）依题意有 t≥8，2t-20≥8，60-t-2t+20≥8，
解得14≤t≤24，
又∵t为正整数，
∴t最大为24，
∵W是关于t的一次函数，由（3）知W随t的增大而增大，
∴当t=24（台）时，W_最大=0.5×24+4.2=16.2（万元），
∴该公司这次向灾区捐款金额的最大值为16.2万元。