题目内容
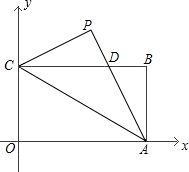 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA=| 3 |
(1)填空:∠PCB=
(2)若P,A两点在抛物线y=-
| 4 |
| 3 |
(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
分析:(1)在直角△OAC中,根据三角函数就可以求出∠CAO的度数,以及∠OCA的度数.而∠PCA=∠OCA∠BCA=∠CAO,则:∠PCB就可以求出.在直角△PCG中,根据三角函数可以求得CG,PG的长,从而得到P的坐标.
(2)P、A两点的坐标容易得到,根据待定系数法就可以求出抛物线的解析式.求出b,c的值.C点的坐标已知,代入函数的解析式,就可以判断是否在函数的图象上.
(3)过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G,根据S△CMP=s△CME+S△PME,四边形MCAP的面积就可以表示成OF的函数,利用函数的性质,就可以求出最值.
(2)P、A两点的坐标容易得到,根据待定系数法就可以求出抛物线的解析式.求出b,c的值.C点的坐标已知,代入函数的解析式,就可以判断是否在函数的图象上.
(3)过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G,根据S△CMP=s△CME+S△PME,四边形MCAP的面积就可以表示成OF的函数,利用函数的性质,就可以求出最值.
解答: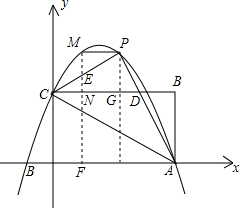 解:(1)30,(
解:(1)30,(
,
)
(2)∵点P(
,
),A(
,0)在抛物线上,
∴
∴
∴抛物线的解析式为y=-
x2+
x+1
C点坐标为(0,1)
∵-
×02+
×0+1=1
∴C点在此抛物线上.
(3)假设存在这样的点M,使得四边形MCAP的面积最大.
∵△ACP面积为定值,
∴要使四边形MCAP的面积最大,只需使△PCM的面积最大.
过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G.
S△CMP=s△CME+S△PME=
ME•CG=
ME
设M(x0,y0),
∵∠ECN=30°,CN=x0,
∴EN=
x0
∴ME=MF-EF=-
x02+
x0
∴S△CMP=-
x02+
x
∵a=-
<0,
∴S有最大值.
当x0=
时,S的最大值是
,
∵S四边形MCAP=s△CPM+S△ACP
∴四边形MCAP的面积的最大值为
此时M点的坐标为(
,
)
所以存在这样的点M(
,
),使得四边形MCAP的面积最大,其最大值为
.
 解:(1)30,(
解:(1)30,(
| ||
| 2 |
| 3 |
| 2 |
(2)∵点P(
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴
|
∴
|
∴抛物线的解析式为y=-
| 4 |
| 3 |
| 3 |
C点坐标为(0,1)
∵-
| 4 |
| 3 |
| 3 |
∴C点在此抛物线上.
(3)假设存在这样的点M,使得四边形MCAP的面积最大.
∵△ACP面积为定值,
∴要使四边形MCAP的面积最大,只需使△PCM的面积最大.
过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G.
S△CMP=s△CME+S△PME=
| 1 |
| 2 |
| ||
| 4 |
设M(x0,y0),
∵∠ECN=30°,CN=x0,
∴EN=
| ||
| 3 |
∴ME=MF-EF=-
| 4 |
| 3 |
2
| ||
| 3 |
∴S△CMP=-
| ||
| 3 |
| 1 |
| 2 |
∵a=-
| ||
| 3 |
∴S有最大值.
当x0=
| ||
| 4 |
| ||
| 16 |
∵S四边形MCAP=s△CPM+S△ACP
∴四边形MCAP的面积的最大值为
9
| ||
| 16 |
此时M点的坐标为(
| ||
| 4 |
| 3 |
| 2 |
所以存在这样的点M(
| ||
| 4 |
| 3 |
| 2 |
9
| ||
| 16 |
点评:本题主要考查了待定系数法求函数的解析式,最值问题基本的解决思路是转化为函数问题.

练习册系列答案
相关题目
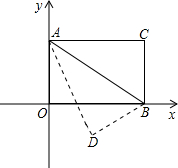 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.


