题目内容
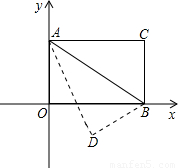
（2002•青海）已知：如图，矩形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A坐标为（0，3），∠OAB=60°，以AB为轴对折后，使C点落在D点处，求D点坐标．
【答案】分析：利用三角函数可得到OB长，根据翻折得到的对应线段相等，也就得到了AD、AC长度，过D向y轴引垂线后，利用三角函数，可得到点D的横坐标，AE的值，进而求得OE的长，点E的纵坐标．
解答：
解：由题意得OA=3，∠OAB=60°，
∴OB=3×tan60°=3
∵△ACB≌△ADB
∴AD=AC=OB，
过D作DE⊥y轴于点E
∵∠OAD=30°
∴ED=
∵cos30°=
那么OE=3
×
-3=1.5
D（
，-1.5）．
点评：翻折前后对应角相等；对应边相等，注意构造直角三角形利用相应的三角函数值求解．
解答：
解：由题意得OA=3，∠OAB=60°，∴OB=3×tan60°=3
∵△ACB≌△ADB
∴AD=AC=OB，
过D作DE⊥y轴于点E
∵∠OAD=30°
∴ED=
∵cos30°=
那么OE=3
×-3=1.5D（
，-1.5）．点评：翻折前后对应角相等；对应边相等，注意构造直角三角形利用相应的三角函数值求解．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
AB；
AB；