题目内容
【题目】如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.求△ABE的面积. 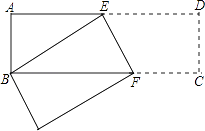
【答案】解:∵四边形ABCD是长方形, ∴∠A=90°,
设BE=xcm,
由折叠的性质可得:DE=BE=xcm,
∴AE=AD﹣DE=9﹣x(cm),
在Rt△ABE中,BE2=AE2+AB2 ,
∴x2=(9﹣x)2+32 ,
解得:x=5,
∴DE=BE=5cm,AE=9﹣x=4(cm),
∴S△ABE= ![]() ABAE=
ABAE= ![]() ×3×4=6(cm2).
×3×4=6(cm2).
【解析】首先设BE=xcm,由折叠的性质可得:DE=BE=xcm,即可得AE=9﹣x(cm),然后在Rt△ABE中,由勾股定理BE2=AE2+AB2 , 可得方程x2=(9﹣x)2+32 , 解此方程即可求得DE的长,继而可得AE的长,则可求得△ABE的面积.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目