题目内容
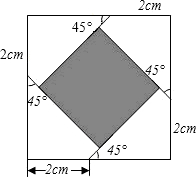 (2009•甘孜州)现有若干张边长不相等但都大于6cm的正方形纸片,从中任选一张,如图从距离正方形的四个顶点2cm处,沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积是
(2009•甘孜州)现有若干张边长不相等但都大于6cm的正方形纸片,从中任选一张,如图从距离正方形的四个顶点2cm处,沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积是8
8
cm2.分析:延长小正方形的一边AB,与大正方形的一边交于C点,连接CD,构造直角边长为2的等腰直角三角形,将小正方形的边长转化为等腰直角三角形的斜边长来求解即可.
解答: 解:如图,延长小正方形的一边AB,与大正方形的一边交于C点,连接CD,
解:如图,延长小正方形的一边AB,与大正方形的一边交于C点,连接CD,
∴△CED为直角边长为2cm的等腰直角三角形,
∴CD=
=
=2
,
∴阴影正方形的边长=AB=2
cm,
∴阴影正方形的面积为:2
×2
=8(cm2).
故答案为:8.
 解:如图,延长小正方形的一边AB,与大正方形的一边交于C点,连接CD,
解:如图,延长小正方形的一边AB,与大正方形的一边交于C点,连接CD,∴△CED为直角边长为2cm的等腰直角三角形,
∴CD=
| DE2+CE2 |
| 4+4 |
| 2 |
∴阴影正方形的边长=AB=2
| 2 |
∴阴影正方形的面积为:2
| 2 |
| 2 |
故答案为:8.
点评:本题主要考查了正方形的性质,勾股定理的应用,关键是正确做出辅助线,求出CD的长,进而得到正方形的边长,同时也渗透了转化思想.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
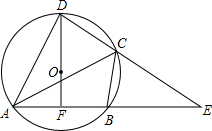 (2009•甘孜州)已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=
(2009•甘孜州)已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=