题目内容
证明：等腰梯形的两条对角线相等．
要求：画图、写已知、求证并证明．
要求：画图、写已知、求证并证明．
分析：画出图形，然后根据图形写出已知，求证，根据等腰梯形同一底上的两底角相等可得∠ABC=∠DCB，然后利用“边角边”证明△ABC和△DCB全等，根据全等三角形对应边相等即可得到AC=BD．
解答：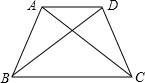
已知：如图，等腰梯形ABCD中，AD∥BC，AB=CD，
求证：AC=BD，
证明：在等腰梯形ABCD中，∠ABC=∠DCB，
在△ABC和△DCB中，
，
∴△ABC≌△DCB（SAS），
∴AC=BD．
已知：如图，等腰梯形ABCD中，AD∥BC，AB=CD，求证：AC=BD，
证明：在等腰梯形ABCD中，∠ABC=∠DCB，
在△ABC和△DCB中，
|
∴△ABC≌△DCB（SAS），
∴AC=BD．
点评：本题考查了等腰梯形对角线相等的证明，熟记等腰梯形同一底上的两底角相等得到三角形全等的条件是解题的关键，求证线段相等，通常证明线段所在的三角形全等是常用的方法，要熟练掌握并灵活运用．
练习册系列答案
相关题目