Question

【题目】如图某人在一斜坡坡脚A处测得电视塔塔尖C的仰角为60°，沿斜坡向上走到P处再测得塔尖C的仰角为45°，若OA=45米，斜坡的坡比(竖直高度与水平高度的比)为1：2，且O、A、B在同一条直线上．求电视塔OC的高度及此人所在位置P到AB的距离．（测角器高度忽略不计，结果精确到0.1米．参考数据：，）

Answer 1

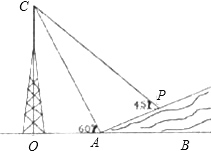
【答案】点P到AB的距离约为11.0米．

【解析】

试题分析：因为直角三角形AOC中知道OA的长度，知道∠OAC=60°，解直角三角形可求出解．作PE⊥OB交OB于E点，PD⊥CO交CO于D点．根据∠PCD为45°，坡度为1：2，设出PE=x．根据线段相等，可列出方程求解．

试题解析：在Rt△COA中，∠OAC=60°，OA=45则OC=OAtan60°=45≈77.9（米）

故电视塔OC高度约为77.9米．

作PD⊥CO于D，PE⊥AB于E

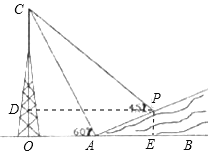
设PE=x，则AE=2x，DO=PE=x，DP=OE=45+2x．

∵∠CPD=45°，

∴∠PCD=45°，则CD=DP．

∴45-x=45+2x，

即3x=45(-1)，

∴x≈11.0（米）．

故点P到AB的距离约为11.0米．（10分）