��Ŀ����
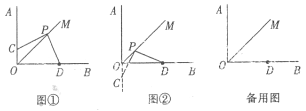
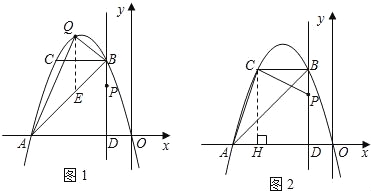
����Ŀ����ͼ������ԭ���������y=��x2��2mx��m��1����x�����һ������ΪA������P����1��m����ֱ��PD��x���ڵ�D�����������ڵ�B��BC��x�ύ�������ڵ�C��

��1����m=2ʱ��
�����߶�BC�ij���ֱ��AB����Ӧ�ĺ�����ϵʽ��
��������Q��ֱ��AB�Ϸ������������˶������Q�ںδ�ʱ����QAB��������
������F���������ϣ���PF=PC����ֱ��д�����������ĵ�F�����ꣻ
��2����m��1ʱ������CA��CP����mΪ��ֵʱ��CA��CP��
���𰸡���1����ֱ��AB����Ӧ�ĺ�����ϵʽΪy=x+4��
����a=-![]() ʱ����QAB��������ʱQ������Ϊ��-
ʱ����QAB��������ʱQ������Ϊ��-![]() ��
��![]() ����
����
�����������ĵ�F����ΪF1����2��0����F2��0��0����F3��0��4����
��2��m=![]() ��
��
��������
�����������1���ٽ�m=2����y=��x2��2mx���ó�y=��x2��4x�����A����4��0����B����1��3������B��C�������������y=��x2��4x�ĶԳ���x=��2�Գƣ��ó�BC=2�����ô���ϵ�������ֱ��AB����Ӧ�ĺ�����ϵʽ��
�ڹ���Q��QE��y�ᣬ��AB�ڵ�E����Q��a����a2��4a������E��a��a+4����QE=����a2��4a������a+4��=��a2��5a��4����S��QAB=![]() QEAD���S��QAB=��
QEAD���S��QAB=��![]() ��a+
��a+![]() ��2+
��2+![]() �����ݶ��κ��������ʼ�����⣻
�����ݶ��κ��������ʼ�����⣻
�۷���������������ۣ�����F��x���ϣ���F��x��0��������PF=PC�г����̣��ⷽ�̵õ�F1����2��0����F2��0��0��������F��y���ϣ���F��0��y��������PF=PC�г����̣��ⷽ�̵õ�F3��0��4����F4��0��0����F2��0��0���غϣ�
��2������C��CH��x���ڵ�H�������PB=m��1��BC=2��m��1����CH=2m��1��AH=1����֤����ACH�ס�PCB���������������ζ�Ӧ�߳ɱ����ó�![]() ����
����![]() ���ⷽ�̿����m��ֵ��
���ⷽ�̿����m��ֵ��
�����������1���ٵ�m=2ʱ��y=��x2��4x��
��y=0���é�x2��4x=0��
���x1=0��x2=��4��
��A����4��0����
��x=��1ʱ��y=3��
��B����1��3����
��������y=��x2��4x�ĶԳ���Ϊֱ��x=��2��
��B��C������ڶԳ���x=��2�Գƣ�
��C����3��3����BC=2��
��ֱ��AB����Ӧ�ĺ�����ϵʽΪy=kx+b��
��A����4��0����B����1��3����ֱ��AB�ϣ�
��![]() �����
�����![]()
��ֱ��AB����Ӧ�ĺ�����ϵʽΪy=x+4��
�ڹ���Q��QE��y�ᣬ��AB�ڵ�E����ͼ1����
���������Q��a����a2��4a������E��a��a+4����
��QE=����a2��4a������a+4��=��a2��5a��4��
��S��QAB=![]() QEAD=
QEAD=![]() ������a2��5a��4����3=��
������a2��5a��4����3=��![]() ��a+
��a+![]() ��2+
��2+![]() ��
��
����a=-![]() ʱ����QAB��������ʱQ������Ϊ��-
ʱ����QAB��������ʱQ������Ϊ��-![]() ��
��![]() ����
����
�۷����������
����F��x���ϣ���F��x��0����
��PF=PC��P����1��2����C����3��3����
����x+1��2+��2��0��2=����3+1��2+��3��2��2��
��������x2+2x=0��
���x1=��2��x2=0��
��F1����2��0����F2��0��0����
����F��y���ϣ���F��0��y����
��PF=PC��P����1��2����C����3��3����
����0+1��2+��y��2��2=����3+1��2+��3��2��2��
��������y2��4y=0��
���y1=4��y2=0��
��F3��0��4����F4��0��0����F2��0��0���غϣ�
�������������������ĵ�F����ΪF1����2��0����F2��0��0����F3��0��4����
��2������C��CH��x���ڵ�H����ͼ2������P����1��m����B����1��2m��1����
��PB=m��1����������y=��x2��2mx�ĶԳ���Ϊֱ��x=��m������m��1��
��B��C������ڶԳ���x=��m�Գƣ���BC=2��m��1����
��C��1��2m��2m��1����H��1��2m��0������CH=2m��1����A����2m��0������AH=1��
����֪������ACP=��BCH=90�㣬���ACH=��PCB�����ߡ�AHC=��PBC=90�㣬
���ACH�ס�PCB����![]() ����
����![]() ����m=
����m=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�