题目内容
【题目】如图，在ABCD中，AC为对角线，AC=BC=5，AB=6，AE是△ABC的中线．
（1）用无刻度的直尺画出△ABC的高CH（保留画图痕迹）；
（2）求△ACE的面积．
【答案】（1）详见解析；（2）6.
【解析】
试题分析：（1）连接BD，BD与AE交于点F，连接CF并延长到AB，与AB交于点H，则CH为△ABC的高；（2）根据等腰三角形三线合一的性质可求得AH的长，再由勾股定理求得CH的长，继而求得△ABC的面积，又由AE是△ABC的中线，求得△ACE的面积．
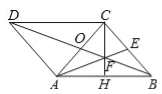
试题解析：（1）如图，连接BD，BD与AE交于点F，连接CF并延长到AB，则它与AB的交点即为H．理由如下：
∵BD、AC是ABCD的对角线，
∴点O是AC的中点，
∵AE、BO是等腰△ABC两腰上的中线，
∴AE=BO，AO=BE，
∵AO=BE，
∴△ABO≌△BAE（SSS），
∴∠ABO=∠BAE，
△ABF中，∵∠FAB=∠FBA，∴FA=FB，
∵∠BAC=∠ABC，
∴∠EAC=∠OBC，
由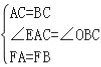
可得△AFC≌BFC（SAS）
∴∠ACF=∠BCF，即CH是等腰△ABC顶角平分线，
所以CH是△ABC的高；
（2）∵AC=BC=5，AB=6，CH⊥AB，
∴AH=
AB=3，
由勾股定理可得CH=4，
∴S△ABC=ABCH=×6×4=12，
∵AE是△ABC的中线，
∴S△ACE=S△ABC=6．
练习册系列答案
相关题目
【题目】某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：
读书时间（小时） | 7 | 8 | 9 | 10 | 11 |
学生人数 | 6 | 10 | 9 | 8 | 7 |
则该班学生一周读书时间的中位数和众数分别是（ ）
A. 9，8 B. 9，9 C. 9.5，9 D. 9.5，8
