题目内容
已知圆锥的侧面展开图的圆心角为120°,则这个圆锥的侧面积是底面积的
- A.2倍
- B.3倍
- C.

- D.

B
分析:设出圆锥的母线长和底面半径,利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而表示出圆锥的侧面积和底面积,比较即可.
解答:设母线长为R,底面半径为r,则底面周长C=2πr.
圆锥的侧面展开是扇形,母线是扇形的半径.
∴扇形面积S扇= =
= =
= =
= CR,
CR,
∴C=2πr=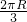 ,
,
∴r=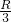 ,
,
∴底面面积S底= ,
,
∴S扇:S底=3,
故选B.
点评:本题利用了扇形的面积公式和圆的面积公式求解.
分析:设出圆锥的母线长和底面半径,利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而表示出圆锥的侧面积和底面积,比较即可.
解答:设母线长为R,底面半径为r,则底面周长C=2πr.
圆锥的侧面展开是扇形,母线是扇形的半径.
∴扇形面积S扇=
 =
= =
= =
= CR,
CR,∴C=2πr=
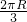 ,
,∴r=
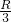 ,
,∴底面面积S底=
 ,
,∴S扇:S底=3,
故选B.
点评:本题利用了扇形的面积公式和圆的面积公式求解.

练习册系列答案
相关题目
已知圆锥的侧面展开图的圆心角为120°,则这个圆锥的侧面积是底面积的( )
| A、2倍 | ||
| B、3倍 | ||
C、
| ||
D、
|