题目内容
已知y是x的二次函数,且其图象在x轴上截得的线段AB长4个单位,当x=3时,y取得最小值-2.(1)求这个二次函数的解析式;
(2)若此函数图象上有一点P,使△PAB的面积等于12个平方单位,求P点坐标.
分析:(1)根据抛物线的对称轴为x=3,以及AB=4,可求得A、B的坐标,然后根据其顶点坐标用顶点式二次函数通式设抛物线的解析式,然后将A或B点的坐标代入抛物线中即可求得二次函数的解析式.
(2)已知了AB的长,可根据三角形的面积求得P点纵坐标的绝对值,然后代入抛物线的解析式中即可求得P点的坐标.
(2)已知了AB的长,可根据三角形的面积求得P点纵坐标的绝对值,然后代入抛物线的解析式中即可求得P点的坐标.
解答: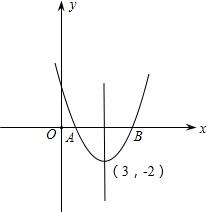 解:(1)∵当x=3时y取得最小值-2.
解:(1)∵当x=3时y取得最小值-2.
即抛物线顶点为(3,-2),对称轴为直线x=3,
∴设二次函数解析式为y=a(x-3)2-2.
又∵图象在x轴上截得线段AB的长是4,
∴图象与x轴交于(1,0)和(5,0)两点.
∴a(1-3)2-2=0,
∴a=
,
∴所求二次函数解析式为y=
x2-3x+
.
(2)∵△PAB的面积为12个平方单位,|AB|=4.
∴
×4×|Py|=12,
∴|Py|=6,
∴Py=±6.
但抛物线开口向上,函数值最小为-2,
∴Py=-6应舍去,
∴Py=6又点P在抛物线上,
∴6=
x2-3x+
,
解得,x1=-1,x2=7.
即点P的坐标为(-1,6)或(7,6).
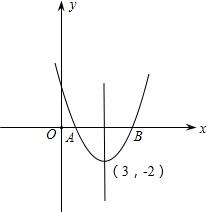 解:(1)∵当x=3时y取得最小值-2.
解:(1)∵当x=3时y取得最小值-2.即抛物线顶点为(3,-2),对称轴为直线x=3,
∴设二次函数解析式为y=a(x-3)2-2.
又∵图象在x轴上截得线段AB的长是4,
∴图象与x轴交于(1,0)和(5,0)两点.
∴a(1-3)2-2=0,
∴a=
| 1 |
| 2 |
∴所求二次函数解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)∵△PAB的面积为12个平方单位,|AB|=4.
∴
| 1 |
| 2 |
∴|Py|=6,
∴Py=±6.
但抛物线开口向上,函数值最小为-2,
∴Py=-6应舍去,
∴Py=6又点P在抛物线上,
∴6=
| 1 |
| 2 |
| 5 |
| 2 |
解得,x1=-1,x2=7.
即点P的坐标为(-1,6)或(7,6).
点评:本题考查了二次函数解析式的确定以及图形面积的求法等知识点.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知y是x的二次函数,函数y与自变量x的部分对应值如下表:
观察表中数据,则k的值为 .
| x | … | -2 | -1 | 1 | 2 | … | |
| y | … | 4 | 6 | 4 | k | … |