题目内容
（2012•滨州一模）计算（或解不等式）：（1）
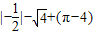
（2）
≤
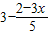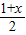
【答案】分析：（1）利用实数的运算求解即可；注意绝对值，算术平方根，0指数幂的求解；
（2）利用不等式的基本性质，解不等式即可求得．
解答：解：（1）原式=
-2+1=-
；
（2）去分母得：30-2（2-3x）≤5（1+x）
去括号得：30-4+6x≤5+5x
移项合并同类项得：x≤-21．
故答案为-
、x≤-21．
点评：（1）考查了实数的运算，注意绝对值，算术平方根，0指数幂的求解；
（2）此题考查了不等式的解法．不等式的解题步骤为：去分母，去括号，移项合并同类项，系数化一．注意系数化一时：不等式的两边同时乘以或除以同一个正数不等号的方向不变；不等式的两边同时乘以或除以同一个负数不等号的方向改变．
（2）利用不等式的基本性质，解不等式即可求得．
解答：解：（1）原式=
-2+1=-；（2）去分母得：30-2（2-3x）≤5（1+x）
去括号得：30-4+6x≤5+5x
移项合并同类项得：x≤-21．
故答案为-
、x≤-21．点评：（1）考查了实数的运算，注意绝对值，算术平方根，0指数幂的求解；
（2）此题考查了不等式的解法．不等式的解题步骤为：去分母，去括号，移项合并同类项，系数化一．注意系数化一时：不等式的两边同时乘以或除以同一个正数不等号的方向不变；不等式的两边同时乘以或除以同一个负数不等号的方向改变．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
（2012•滨州一模）已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：
现将两种食物混合成100千克的混合食品．设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位．
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
（2012•滨州一模）已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：
现将两种食物混合成100千克的混合食品．设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位．
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．