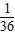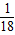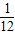题目内容
（2012•滨州一模）如图，任意一个凸四边形ABCD，E、F、G、H分别是各边的中点，图中阴影部分的两块面积之和是四边形ABCD的面积的 ．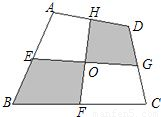
【答案】分析：分别连接OB、OA、OD、OC，根据E、F、G、H分别是AB、BC、CD、DA的中点，利用三角形同底同高的特点，求证S△AOH=S△DOH，S△AOE=S△EOB，S△BOF=S△COF，S△DOG=S△COG，再将S△AOH+S△AOE+S△COF+S△COG即为阴影部分面积．
解答：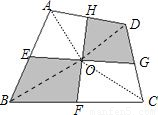
解：分别连接OB、OA、OD、OC，
∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴S△AOH=S△DOH，S△AOE=S△EOB，
S△BOF=S△COF，S△DOG=S△COG，
S△AOH+S△AOE+S△COF+S△COG=
S四边形ABCD，
即图中阴影部分的总面积为=
S四边形ABCD，
故答案为
．
点评：此题主要考查学生对三角形面积的计算，解答此题的关键是分别连接OB、OA、OD、OC，利用三角同底同高的性质求证几个三角形面积相等，此题有一定难度，属于难题．
解答：
解：分别连接OB、OA、OD、OC，∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴S△AOH=S△DOH，S△AOE=S△EOB，
S△BOF=S△COF，S△DOG=S△COG，
S△AOH+S△AOE+S△COF+S△COG=
S四边形ABCD，即图中阴影部分的总面积为=
S四边形ABCD，故答案为
．点评：此题主要考查学生对三角形面积的计算，解答此题的关键是分别连接OB、OA、OD、OC，利用三角同底同高的性质求证几个三角形面积相等，此题有一定难度，属于难题．
练习册系列答案
相关题目
（2012•滨州一模）已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：
现将两种食物混合成100千克的混合食品．设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位．
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
（2012•滨州一模）已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：
现将两种食物混合成100千克的混合食品．设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位．
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．