Question

（2013•内江）同时抛掷A、B两个均匀的小立方体（每个面上分别标有数字1，2，3，4，5，6），设两立方体朝上的数字分别为x、y，并以此确定点P（x，y），那么点P落在抛物线y=-x²+3x上的概率为（　　）

• A．

  1

  18

• B．

  1

  12

• C．

  1

  9

• D．

  1

  6

Answer 1

分析：画出树状图，再求出在抛物线上的点的坐标的个数，然后根据概率公式列式计算即可得解．

解答：解：根据题意，画出树状图如下：

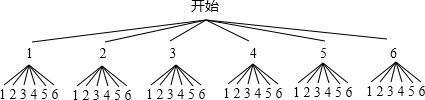
一共有36种情况，
当x=1时，y=-x²+3x=-1²+3×1=2，
当x=2时，y=-x²+3x=-2²+3×2=2，
当x=3时，y=-x²+3x=-3²+3×3=0，
当x=4时，y=-x²+3x=-4²+3×4=-4，
当x=5时，y=-x²+3x=-5²+3×5=-10，
当x=6时，y=-x²+3x=-6²+3×6=-18，
所以，点在抛物线上的情况有2种，
P（点在抛物线上）=

2

36

=

1

18

．
故选A．

点评：本题考查了列表法与树状图法，二次函数图象上点的坐标特征，用到的知识点为：概率=所求情况数与总情况数之比．