题目内容
某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价y1与月份x（1≤x≤7，且x为整数），之间的函数关系式如下表：| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y1（元/千克） | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
（1）请观察表格和图象，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出y1与x和y2与x的函数关系式．
（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量p1（千克）与月份x满足：p1=10x+80；8月至12月的销量p2（千克）与月份x满足：p2=-10x+250；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润．
（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了a%（a＜100），与此同时每月的销量均在去年12月的基础上减少了0.2a%，这样销售下去要使今年1至6月的总利润为68130元，试求出a的值．（保留两个有效数字）（参考数据：232=529，242=576，252=625，262=676）
分析：（1）利用待定系数法分别将（1，50），（2，60）和（8，15）（12，135）分别代入得出解析式即可；
（2）根据所获得的利润=销售数量×（售价-进价），就可以表示出销售利润与月份之间的函数关系式进而求出最值即可；
（3）利用上年12月份的进价，固定支出以及销量表示出今年的进价，固定支出以及销量即可得出关于1至6月的总利润的方程，进而求出a即可．
（2）根据所获得的利润=销售数量×（售价-进价），就可以表示出销售利润与月份之间的函数关系式进而求出最值即可；
（3）利用上年12月份的进价，固定支出以及销量表示出今年的进价，固定支出以及销量即可得出关于1至6月的总利润的方程，进而求出a即可．
解答：解：（1）由表格可知，y1是x的一次函数．
设y1=k1x+b1（k1≠0）．
将（1，50），（2，60）分别代入得：
解这个方程组得
∴y1=10x+40．
经验证其余各组值也均满足此函数关系式．
∴y1=10x+40．
设y2=k2x+b2（k2≠0）．
将坐标（8，15）（12，135）分别代入得：
解得：
，
故y2=5x+75．
（2）设：利润为W元．
当1≤x≤7时，
W1=（180-10x-40）•（10x+80）-300，
=（-10x+140）（10x+800）-300，
=-100x 2+600x+10900，
-
=-
=3．
∴当x=3时，W1有最大值，W1大=11800．
当8≤x≤12时，
W2=（180-5x-75）（-10x+250）-300
=（-5x+105）（-10x+250）-300
=50x2-2300x+25950．
∵-
=-
=23，又x＜23，
∴W2随x增大而减小，∴x=8时，W2有最大值，
W2大=10750．
∵W1大＞W2大
∴在第3月时，可获最大利润11800．
（3）根据题意可得出：6×[180（1+a%）-（5×12+75+15）]•（-10×12+250）（1-0.2a%）-6×300（1+15%）=68130．
令a%=t，原方程化为[6（1+t）-5]（1-
t）-3=0．
整理得 6t2-29t+10=0．∴t=
≈
．
则t1=
=
≈33.3%，t2=
=450%．
∴a1≈33，a2=450（舍）．
∴a=33．
即：a的值为33．
设y1=k1x+b1（k1≠0）．
将（1，50），（2，60）分别代入得：
|
解这个方程组得
|
∴y1=10x+40．
经验证其余各组值也均满足此函数关系式．
∴y1=10x+40．
设y2=k2x+b2（k2≠0）．
将坐标（8，15）（12，135）分别代入得：
|
|
故y2=5x+75．
（2）设：利润为W元．
当1≤x≤7时，
W1=（180-10x-40）•（10x+80）-300，
=（-10x+140）（10x+800）-300，
=-100x 2+600x+10900，
-
| b |
| 2a |
| 600 |
| -200 |
∴当x=3时，W1有最大值，W1大=11800．
当8≤x≤12时，
W2=（180-5x-75）（-10x+250）-300
=（-5x+105）（-10x+250）-300
=50x2-2300x+25950．
∵-
| b |
| 2a |
| -2300 |
| 100 |
∴W2随x增大而减小，∴x=8时，W2有最大值，
W2大=10750．
∵W1大＞W2大
∴在第3月时，可获最大利润11800．
（3）根据题意可得出：6×[180（1+a%）-（5×12+75+15）]•（-10×12+250）（1-0.2a%）-6×300（1+15%）=68130．
令a%=t，原方程化为[6（1+t）-5]（1-
| 1 |
| 5 |
整理得 6t2-29t+10=0．∴t=
29±
| ||
| 12 |
| 29±25 |
| 12 |
则t1=
| 4 |
| 12 |
| 1 |
| 3 |
| 54 |
| 12 |
∴a1≈33，a2=450（舍）．
∴a=33．
即：a的值为33．
点评：此题主要考查了二次函数的综合试题以及待定系数法求反比例函数的解析式和一次函数的解析式，根据一次函数的解析式和二次函数的解析式求最值的运用及一元二次方程的解法及运用．
练习册系列答案
相关题目
某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价
与月份
（
，且为整数），之间的函数关系式如下表 ：
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 50 | 60 | 70 | 80 | 90 | 100 | 110 |
随着我国对一些国家进出口关税的调整，该水果的进价涨势趋缓，在8至12月份每千克水果A的进价
与月份（
，且为整数）之间存在如下图所示的变化趋势.
（1）请观察表格和图像，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出 与和与的函数关系式.
（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量
（千克）与月份满足：
；8月至12月的销量
（千克）与月份满足：
；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润.
（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了
（
<100），与此同时每月的销量均在去年12月的基础上减少了
，这样销售下去要使今年1至6月的总利润为68130元，试求出的值.（保留两个有效数字）（参考数据：
， 
，
）
某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价
与月份
（
，且为整数），之间的函数关系式如下表 ：
随着我国对一些国家进出口关税的调整，该水果的进价涨势趋缓，在8至12月份每千克水果A的进价
与月份（
，且为整数）之间存在如下图所示的变化趋势.
（1）请观察表格和图像，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出 与和与的函数关系式.
（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量
（千克）与月份满足：
；8月至12月的销量
（千克）与月份满足：
；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润.
（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了
（
<100），与此同时每月的销量均在去年12月的基础上减少了
，这样销售下去要使今年1至6月的总利润为68130元，试求出的值.（保留两个有效数字）（参考数据：
，
，
）
与月份（，且为整数），之间的函数关系式如下表 ：| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| （元/千克） | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
与月份（，且为整数）之间存在如下图所示的变化趋势.（1）请观察表格和图像，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出
与和与的函数关系式.（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量
（千克）与月份满足：；8月至12月的销量（千克）与月份满足：；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润.（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了
（<100），与此同时每月的销量均在去年12月的基础上减少了，这样销售下去要使今年1至6月的总利润为68130元，试求出的值.（保留两个有效数字）（参考数据： ，，） 某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价
与月份
（
，且为整数），之间的函数关系式如下表 ：
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| （元/千克） | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
与月份（
，且为整数）之间存在如下图所示的变化趋势.（1）请观察表格和图像，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出
与和与的函数关系式.（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量
（千克）与月份满足：
；8月至12月的销量
（千克）与月份满足：
；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润.（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了
（
<100），与此同时每月的销量均在去年12月的基础上减少了
，这样销售下去要使今年1至6月的总利润为68130元，试求出的值.（保留两个有效数字）（参考数据：
，
，
）
某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价y1与月份x（1≤x≤7，且x为整数），之间的函数关系式如下表：
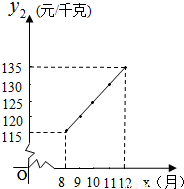
随着我国对一些国家进出口关税的调整，该水果的进价涨势趋缓，在8至12月份每千克水果A的进价y2与月份x（8≤x≤12，且x为整数）之间存在如下图所示的变化趋势．
（1）请观察表格和图象，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出y1与x和y2与x的函数关系式．
（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量p1（千克）与月份x满足：p1=10x+80；8月至12月的销量p2（千克）与月份x满足：p2=-10x+250；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润．
（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了a%（a＜100），与此同时每月的销量均在去年12月的基础上减少了0.2a%，这样销售下去要使今年1至6月的总利润为68130元，试求出a的值．（保留两个有效数字）（参考数据：232=529，242=576，252=625，262=676）
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y1（元/千克） | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
（1）请观察表格和图象，用所学过的一次函数、反比例函数、二次函数的有关知识分别写出y1与x和y2与x的函数关系式．
（2）若去年该水果的售价为每千克180元，且销售该水果每月必须支出（除进价外）的固定支出为300元，已知该水果在1月至7月的销量p1（千克）与月份x满足：p1=10x+80；8月至12月的销量p2（千克）与月份x满足：p2=-10x+250；则该水果在第几月销售时，可使该月所获得的利润最大？并求出此时的最大利润．
（3）今年1月到6月，该进口水果的进价进行调整，每月进价均比去年12月的进价上涨15元，且每月的固定支出（除进价外）增加了15%，已知该进口水果的售价在去年的基础上提高了a%（a＜100），与此同时每月的销量均在去年12月的基础上减少了0.2a%，这样销售下去要使今年1至6月的总利润为68130元，试求出a的值．（保留两个有效数字）（参考数据：232=529，242=576，252=625，262=676）