题目内容
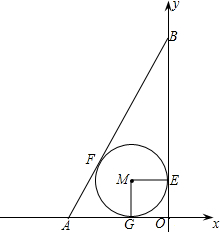 如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式.
如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式.
分析:要求直线l对应的一次函数的表达式,由直线l经过点D(-1,4),根据待定系数法,只需求出此直线上另外一点F的坐标即可.设直角△AOB的内切圆⊙M与OA、OB、AB分别切于点G、E、F.先由直角△AOB的内切圆的面积为π,得出其内切圆面积为1,易证四边形OGME是正方形,得出点G的坐标为(-1,0).再延长GM交AB于N,证明点N与点D重合.然后过点F作FP⊥OB于P,交GN于H.分别解RT△MNF和RT△HNF,求出点F的坐标.
解答: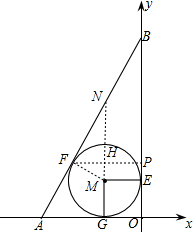 解:设直角△AOB的内切圆⊙M与OA、OB、AB分别切于点G、E、F,则∠MGO=∠MFB=∠OEM=90°.
解:设直角△AOB的内切圆⊙M与OA、OB、AB分别切于点G、E、F,则∠MGO=∠MFB=∠OEM=90°.
∵⊙M的面积为π,
∴π×ME2=π,
∴ME=1.
∵∠MGO=∠GOE=∠OEM=90°,MG=ME,
∴四边形OGME是正方形,
∴OG=1,点G的坐标为(-1,0).
延长GM交AB于N,则NG⊥OA,
∴N点横坐标与G点横坐标相同,是-1,
又∵直线AB经过点D(-1,4),
∴点N与点D重合.
∴MN=NG-MG=4-1=3.
在RT△MNF中,MN=3,MF=1,
由勾股定理,可知FN=2
.
∴sin∠FNM=
,tan∠FNM=
=
.
过点F作FP⊥OB于P,交GN于H,则FP=FH+HP=FH+ME=FH+1,HG=HM+MG=HM+1.
在Rt△HNF中,∠FHN=90°,FN=2
,sin∠FNH=
,
∴FH=FN•sin∠FNH=
,
∴FP=
+1=
;
在RT△MHF中,∠FHN=90°,FH=
,tan∠MFH=tan∠FNM=
,
∴HM=FH•tan∠MFH=
×
=
,
∴HG=
+1=
,
∴点F的坐标为(-
,
).
设直线l的解析式为y=kx+b.
∵直线l经过点D(-1,4),点F(-
,
),
∴
,
解得
.
故所求直线l的解析式为y=2
x+4+2
.
 解:设直角△AOB的内切圆⊙M与OA、OB、AB分别切于点G、E、F,则∠MGO=∠MFB=∠OEM=90°.
解:设直角△AOB的内切圆⊙M与OA、OB、AB分别切于点G、E、F,则∠MGO=∠MFB=∠OEM=90°.∵⊙M的面积为π,
∴π×ME2=π,
∴ME=1.
∵∠MGO=∠GOE=∠OEM=90°,MG=ME,
∴四边形OGME是正方形,
∴OG=1,点G的坐标为(-1,0).
延长GM交AB于N,则NG⊥OA,
∴N点横坐标与G点横坐标相同,是-1,
又∵直线AB经过点D(-1,4),
∴点N与点D重合.
∴MN=NG-MG=4-1=3.
在RT△MNF中,MN=3,MF=1,
由勾股定理,可知FN=2
| 2 |
∴sin∠FNM=
| 1 |
| 3 |
| 1 | ||
2
|
| ||
| 4 |
过点F作FP⊥OB于P,交GN于H,则FP=FH+HP=FH+ME=FH+1,HG=HM+MG=HM+1.
在Rt△HNF中,∠FHN=90°,FN=2
| 2 |
| 1 |
| 3 |
∴FH=FN•sin∠FNH=
2
| ||
| 3 |
∴FP=
2
| ||
| 3 |
2
| ||
| 3 |
在RT△MHF中,∠FHN=90°,FH=
2
| ||
| 3 |
| ||
| 4 |
∴HM=FH•tan∠MFH=
2
| ||
| 3 |
| ||
| 4 |
| 1 |
| 3 |
∴HG=
| 1 |
| 3 |
| 4 |
| 3 |
∴点F的坐标为(-
2
| ||
| 3 |
| 4 |
| 3 |
设直线l的解析式为y=kx+b.
∵直线l经过点D(-1,4),点F(-
2
| ||
| 3 |
| 4 |
| 3 |
∴
|
解得
|
故所求直线l的解析式为y=2
| 2 |
| 2 |
点评:本题主要考查了直角三角形内切圆半径的求法,切线的性质,正方形的判定与性质,解直角三角形及运用待定系数法求一次函数的解析式,综合性较强,有一定难度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 )作x轴的平行线分别交双曲线y=
)作x轴的平行线分别交双曲线y= (2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=
(2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=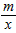 (x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交双曲线y=
(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交双曲线y=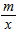 (x>0)和y=-
(x>0)和y=-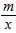 (x<0)于点M、N。
(x<0)于点M、N。
 经过点
经过点 和点
和点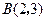 ,另一条直线
,另一条直线

 ,且与
,且与 轴相交于点
轴相交于点 .
. 的面积为3,求
的面积为3,求 的值.
的值.