题目内容
 (2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=
(2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=| m |
| x |
| m |
| x |
| m |
| x |
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA.
分析:(1)将点B(2,1)代入y=
,即可求出m的值,从而得到反比例函数的解析式;将点A(1,0),点B(2,1)分别代入y=kx+b,即可求出l的解析式;
(2)点P(a,a-1)(a>1)在直线y=2上,即可得到a-1=2,从而求出a的值,得到P点坐标,作出直线MN,连接MB、NA,即可构造三角形△PMB和△PNA,然后根据对应线段成比例证出△PMB∽△PNA.
| m |
| x |
(2)点P(a,a-1)(a>1)在直线y=2上,即可得到a-1=2,从而求出a的值,得到P点坐标,作出直线MN,连接MB、NA,即可构造三角形△PMB和△PNA,然后根据对应线段成比例证出△PMB∽△PNA.
解答:解:(1)由点B(2,1)在y=
上,有2=
,即m=2.
设直线l的解析式为y=kx+b,
由点A(1,0),点B(2,1)在y=kx+b上,
得
解之,得
,
∴所求直线l的解析式为y=x-1.
(2)∵点P(a,a-1)(a>1)在直线y=2上,
∴P(3,2),
∴P在直线l上,是直线y=2和l的交点,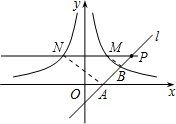
∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2).
∴NP=3-(-1)=4,MP=3-1=2,
AP=
=
=2
,BP=
=
,
∴
=
=2,
在△PMB和△PNA中,∠MPB=∠NPA,
∴△PMB∽△PNA.
| m |
| x |
| m |
| 1 |
设直线l的解析式为y=kx+b,
由点A(1,0),点B(2,1)在y=kx+b上,
得
|
解之,得
|
∴所求直线l的解析式为y=x-1.
(2)∵点P(a,a-1)(a>1)在直线y=2上,
∴P(3,2),
∴P在直线l上,是直线y=2和l的交点,

∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2).
∴NP=3-(-1)=4,MP=3-1=2,
AP=
| 22+22 |
| 8 |
| 2 |
| 12+12 |
| 2 |
∴
| NP |
| MP |
| AP |
| BP |
在△PMB和△PNA中,∠MPB=∠NPA,
∴△PMB∽△PNA.
点评:本题考查了反比例函数综合题,学会待定系数法以及熟悉相似三角形的判定是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目