题目内容
【题目】已知二次函数的图象经过点（0，5）、（1，﹣1）、（2，﹣3）三点
（1）求二次函数的关系式；
（2）求出函数的顶点坐标，与x轴的交点坐标．
【答案】（1）y=2x2﹣8x+5；（2）顶点坐标为（2，﹣3），坐标为（2+
，0）与（2﹣，0）．
【解析】
试题分析：（1）设出二次函数解析式，将三点坐标代入确定出即可；
（2）利用二次函数性质确定出顶点坐标，以及与x轴交点坐标即可．
试题解析：（1）设二次函数解析式为y=ax2+bx+c（a≠0），
把（0，5）、（1，﹣1）、（2，﹣3）三点代入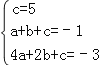得：
，解得：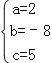
，
则二次函数解析式为y=2x2﹣8x+5；
（2）y=2x2﹣8x+5=2（x﹣2）2﹣3，
令y=0，得到x=2±，
则二次函数顶点坐标为（2，﹣3），与x轴交点坐标为（2+，0）与（2﹣，0）．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
