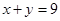题目内容
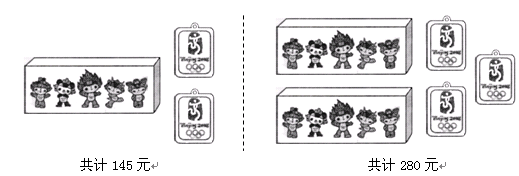
某班有若干人参加一次智力竞赛，共a、b、c三题，每题或者得满分或者得0分. 其中题a、题b、题c满分分别为20分、 30分、40分. 竞赛结果，每个学生至少答对了一题，三题全答对的有1人，只答对其中两道题的有15人，答对题a的人数与答对题b的人数之和为29，答对题a的人数与答对题c的人数之和为25，答对题b的人数与答对题c的人数之和为20，则这个班参赛同学的平均成绩是 分.
51
试题分析：假设xa、xb、xc分别表示答对题a、题b、题c的人数．根据：答对题a的人数与答对题b的人数之和为29，答对题a的人数与答对题c的人数之和为25，答对题b的人数与答对题c的人数之和为20，列出三元一次方程组，求出方程组的解．再根据：竞赛结果，每个学生至少答对了一题，三题全答对的有1人，答对其中两道题的有15人，求得答对1题的人数，进而求出该班总人数．再根据每题分数，求得平均成绩．解：设xa、xb、xc分别表示答对题a、题b、题c的人数．则有
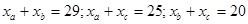由①+②+③得xa+xb+xc=37 ④由④-①得xc=8同理可得xa=17，xb=12∴答对一题的人数为37-1×3-2×15=4，全班人数为1+4+15=20∴平均成绩为51点评：本题属于综合运用题，需要考生对该题在对知识点的熟练把握上解题
练习册系列答案
相关题目
的解是
，求方程组
的解”提出各自的想法．甲说：“这个题目好像条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组中两个方程的两边都除以9，通过换元替代的方法来解决”．参照他们的讨论，你认为这个题目的解应该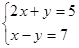是 ．
的解是 ．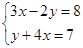
时，一同学把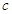
看错而得到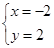
，正确的解应是
，那么
的值是（ ）
可得出
与
的关系式是（ ）
