题目内容

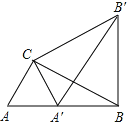
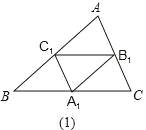
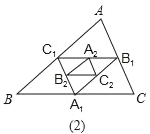
【题目】如图，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB上的点，且A1C1∥AC，A1B1∥AB，B1C1∥BC，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1上的点，且A2C2∥A1C1，A2B2∥A1B1，B2C2∥B1C1，…，按此规律，则第n个图形中平行四边形的个数共有__个．

【答案】3n

【解析】在图(1)中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，

∴A1C1∥AB1A1B1∥BC1A1C1∥B1C

A1C1=AB1A1B1=BC1A1C1=B1C，

∴四边形A1B1AC1、A1B1C1B、A1C1B1C是平行四边形，共有3个。

在图(2)中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，

同理可证：四边形A1B1AC1、A1B1C1B、A1C1B1C、A2B2C2B1、A2B2A1C2、A2C2B2C1是平行四边形，共有6个。

…

按此规律，则第n个图形中平行四边形的个数共有3n个.

故答案为：3n.

练习册系列答案
相关题目

【题目】某商店需要购进A．B两种商品共160件，其进价和售价如表：

A

B

进价（元/件）

15

35

售价（元/件）

20

45

（1）当A．B两种商品分别购进多少件时，商店计划售完这批商品后能获利1100元；

（2）若商店计划购进A种商品不少于66件，且销售完这批商品后获利多于1260元，请你帮该商店老板预算有几种购货方案？获利最大是多少元？

【题目】如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P2017的坐标是（　　）

A. （671，﹣1） B. （672，0） C. （672，1） D. （672，﹣1）

【题目】如图,∠MON为锐角.下列说法:①∠MOP=∠MON;②∠MOP=∠NOP=∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( 　)

A. 1个 B. 2个 C. 3个 D. 4个

【题目】如图，如果直线l上依次有3个点A、B、C，那么

（1）在直线l上共有多少射线？多少条线段？

（2）在直线l上增加一个点，共增加了多少条射线？多少条线段？

（3）如果在直线l上增加到n个点，则共有多少条射线？多少条线段？

【题目】如图，在 ABCD中，∠DAB＝60°，点E，F分别在CD，AB的延长线上，且AE＝AD，CF＝CB．

（1）求证：四边形AFCE是平行四边形．

（2）若去掉已知条件的“∠DAB＝60°，上述的结论还成立吗 ”若成立，请写出证明过程；若不成立，请说明理由．

【题目】如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（ ）
A.3
B.2
C.2
D.2

【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，连接BB′，则BB′的长度为

【题目】某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：

（1）请你根据左图填写右表：

销售公司

平均数

方差

中位数

众数

甲

9

乙

9

17.0

8

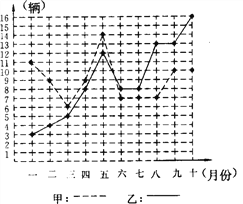
（2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：

①从平均数和方差结合看；

②从折线图上甲、乙两个汽车销售公司销售数量的趋势

看（分析哪个汽车销售公司较有潜力）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网