题目内容
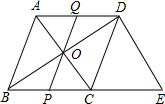 在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E.
在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E.(1)求△BDE的周长;
(2)点P为线段BC上的点,连接PO并延长交AD于点Q.求证:BP=DQ.
分析:(1)因为菱形的对角线互相垂直及互相平分就可以在Rt△AOB中利用勾股定理求出OB,然后利用平行四边形的判定及性质就可以求出△BDE的周长;
(2)容易证明△DOQ≌△BOP,再利用它们对应边相等就可以了.
(2)容易证明△DOQ≌△BOP,再利用它们对应边相等就可以了.
解答:(1)解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,AC⊥BD,OB=OD,OA=OC=3
∴OB=
=4,BD=2OB=8,
∵AD∥CE,AC∥DE,
∴四边形ACED是平行四边形,
∴CE=AD=BC=5,DE=AC=6,
∴△BDE的周长是:BD+BC+CE+DE=8+10+6=24.
(2)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠QDO=∠PBO,
∵在△DOQ和△BOP中
,
∴△DOQ≌△BOP(ASA),
∴BP=DQ.
∴AB=BC=CD=AD=5,AC⊥BD,OB=OD,OA=OC=3
∴OB=
| AB2-OA2 |
∵AD∥CE,AC∥DE,
∴四边形ACED是平行四边形,
∴CE=AD=BC=5,DE=AC=6,
∴△BDE的周长是:BD+BC+CE+DE=8+10+6=24.
(2)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠QDO=∠PBO,
∵在△DOQ和△BOP中
|
∴△DOQ≌△BOP(ASA),
∴BP=DQ.

点评:本题主要利用菱形的对角线互相垂直平分及勾股定理来解决,也考查了全等三角形的判定及性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
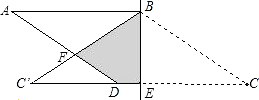 如图,在菱形ABCD中,BE⊥CD于点E,AB=5,BE=3,把菱形沿着BE对折,使点C落在点C′处,则重叠部分(即阴影部分)的面积是
如图,在菱形ABCD中,BE⊥CD于点E,AB=5,BE=3,把菱形沿着BE对折,使点C落在点C′处,则重叠部分(即阴影部分)的面积是 (2012•玉林)如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC≠BD,则图中全等三角形有( )
(2012•玉林)如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC≠BD,则图中全等三角形有( ) (2012•百色)如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF.
(2012•百色)如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF.
