题目内容
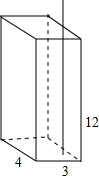 如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为
如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为
- A.3<h<4
- B.3≤h≤4
- C.2≤h≤4
- D.h=4
B
分析:根据题中已知条件,首先要考虑吸管放进杯里垂直于底面时露在杯口外的长度最长为16-12=4cm;最短时与底面对角线和高正好组成直角三角形,用勾股定理解答进而求出露在杯口外的长度最短.
解答:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16-12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为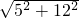 =13cm,则露在杯口外的长度最长为16-13=3cm;
=13cm,则露在杯口外的长度最长为16-13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选B.
点评:本题考查了矩形中勾股定理的运用,解答此题的关键是要找出管最长和最短时在杯中所处的位置,然后计算求解.
分析:根据题中已知条件,首先要考虑吸管放进杯里垂直于底面时露在杯口外的长度最长为16-12=4cm;最短时与底面对角线和高正好组成直角三角形,用勾股定理解答进而求出露在杯口外的长度最短.
解答:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16-12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为
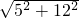 =13cm,则露在杯口外的长度最长为16-13=3cm;
=13cm,则露在杯口外的长度最长为16-13=3cm;则可得露在杯口外的长度在3cm和4cm范围变化.
故选B.
点评:本题考查了矩形中勾股定理的运用,解答此题的关键是要找出管最长和最短时在杯中所处的位置,然后计算求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
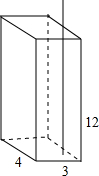 如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )