题目内容
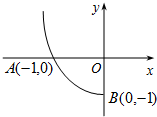 已知,抛物线y=ax2+bx+c(a≠0)经过A、B两点,图中的曲线是它的一部分.根据图中提供的信息,
已知,抛物线y=ax2+bx+c(a≠0)经过A、B两点,图中的曲线是它的一部分.根据图中提供的信息,
(1)确定a,b,c的符号;
(2)当b变化时,求a+b+c的取值范围.
解:(1)如图,由抛物线开口向上,得a>0.
由抛物线过点(0,-1),得c=-1<0.
∵抛物线在y轴左侧没有最低点,
∴抛物线对称轴在y轴的右侧或是y轴,得- ≥0,
≥0,
又a>0,得b≤0.
∴a>0,b≤0,c<0;
(2)由抛物线过点(-1,0),得a-b+c=0.
即a=b-c=b+1,由a>0,得b>-1.
∴-1<b<0,
∴a+b+c=(b+1)+b-1=2b.
∴-2<a+b+c<0.
分析:(1)根据开口方向可确定a的符号;与y轴交于负半轴,所以判定c<0;由抛物线对称轴在y轴的右侧,得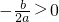 ,又a>0,得b<0.
,又a>0,得b<0.
(2)由抛物线过点(-1,0),得a-b+c=0.进而求得a+b+c的取值范围.
点评:本题考查了二次函数的图象与系数之间的关系,解决本类题目的关键是弄清其系数与图象的关系.
由抛物线过点(0,-1),得c=-1<0.
∵抛物线在y轴左侧没有最低点,
∴抛物线对称轴在y轴的右侧或是y轴,得-
 ≥0,
≥0,又a>0,得b≤0.
∴a>0,b≤0,c<0;
(2)由抛物线过点(-1,0),得a-b+c=0.
即a=b-c=b+1,由a>0,得b>-1.
∴-1<b<0,
∴a+b+c=(b+1)+b-1=2b.
∴-2<a+b+c<0.
分析:(1)根据开口方向可确定a的符号;与y轴交于负半轴,所以判定c<0;由抛物线对称轴在y轴的右侧,得
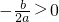 ,又a>0,得b<0.
,又a>0,得b<0.(2)由抛物线过点(-1,0),得a-b+c=0.进而求得a+b+c的取值范围.
点评:本题考查了二次函数的图象与系数之间的关系,解决本类题目的关键是弄清其系数与图象的关系.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
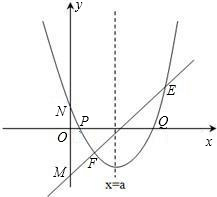 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.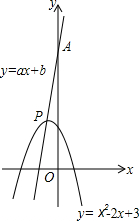 (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.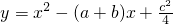 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否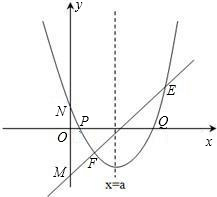 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.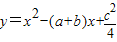 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.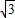 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.