题目内容
△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.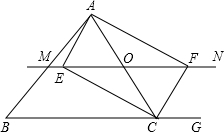
(1)试证明:△CEF为直角三角形.
(2)试证明:OE=OF.
(3)当点O运动到线段AC的中点时,四边形AECF是否是矩形?并证明.
(4)在(3)的条件下,当△ABC为直角三角形且∠ACB=90°,试猜想四边形AECF是什么四边形,并证明.
(1)证明:∵∠ACB的平分线CE,∠ACB的外角平分线CF,
∴∠ECF= ×180°=90°,
×180°=90°,
∴△CEF是直角三角形.
(2)证明:∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠OCE=∠OEC,
∴OC=OE,
同理OC=OF,
∴OE=OF.
(3)答:当点O运动到线段AC的中点时,四边形AECF是矩形,
证明:∵OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵OC=OE=OF=OA,
∴AC=EF,
∴四边形AECF是矩形.
(4)答:四边形AECF是正方形.
证明:∵∠ACB=90°,CE平分∠ACB,
∴∠ACE=45°,
∵∠E=90°,
∴∠EAC=45°=∠ACE,
∴AE=CE,
∵四边形AECF是矩形,
∴四边形AECF是正方形.
分析:(1)关键角平分线性质求出∠FCE=90°即可;
(2)关键平行线性质和角平分线性质求出∠OCE=∠OEC,推出OC=OE,同理求出OC=OF即可;
(3)关键平行四边形的判定推出是平行四边形,求出对角线相等即可;
(4)证出AE=CE即可.
点评:本题主要考查对矩形、正方形、平行四边形的判定,平行线的性质,等腰三角形的性质和判定等知识点的理解和掌握,能灵活运用性质进行推理是解此题的关键.
∴∠ECF=
 ×180°=90°,
×180°=90°,∴△CEF是直角三角形.
(2)证明:∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠OCE=∠OEC,
∴OC=OE,
同理OC=OF,
∴OE=OF.
(3)答:当点O运动到线段AC的中点时,四边形AECF是矩形,
证明:∵OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵OC=OE=OF=OA,
∴AC=EF,
∴四边形AECF是矩形.
(4)答:四边形AECF是正方形.
证明:∵∠ACB=90°,CE平分∠ACB,
∴∠ACE=45°,
∵∠E=90°,
∴∠EAC=45°=∠ACE,
∴AE=CE,
∵四边形AECF是矩形,
∴四边形AECF是正方形.
分析:(1)关键角平分线性质求出∠FCE=90°即可;
(2)关键平行线性质和角平分线性质求出∠OCE=∠OEC,推出OC=OE,同理求出OC=OF即可;
(3)关键平行四边形的判定推出是平行四边形,求出对角线相等即可;
(4)证出AE=CE即可.
点评:本题主要考查对矩形、正方形、平行四边形的判定,平行线的性质,等腰三角形的性质和判定等知识点的理解和掌握,能灵活运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
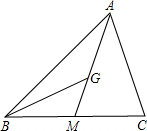 如图,在△ABC中,点G是重心,那么
如图,在△ABC中,点G是重心,那么 26、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
26、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. (2012•本溪)如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE.
(2012•本溪)如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE.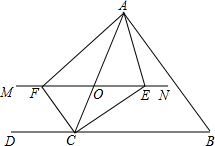 已知:如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交外角∠DCA的平分线于点F,连接AE、AF.
已知:如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交外角∠DCA的平分线于点F,连接AE、AF.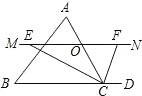 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.探究:线段OE与OF的数量关系,并说明理由.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.探究:线段OE与OF的数量关系,并说明理由.