题目内容
 (2012•陕西)如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为
(2012•陕西)如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为| 41 |
| 41 |
分析:首先过点B作BD⊥x轴于D,由A(0,2),B(4,3),即可得OA=2,BD=3,OD=4,由题意易证得△AOC∽△BDC,根据相似三角形的对应边成比例,即可得OA:BD=OC:DC=AC:BC=2:3,又由勾股定理即可求得这束光从点A到点B所经过的路径的长.
解答: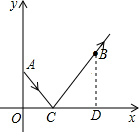 解:如图,过点B作BD⊥x轴于D,
解:如图,过点B作BD⊥x轴于D,
∵A(0,2),B(4,3),
∴OA=2,BD=3,OD=4,
根据题意得:∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴OA:BD=OC:DC=AC:BC=2:3,
∴OC=
OD=
×4=
,
∴AC=
=
,
∴BC=
,
∴AC+BC=
.
即这束光从点A到点B所经过的路径的长为:
.
故答案为:
.
 解:如图,过点B作BD⊥x轴于D,
解:如图,过点B作BD⊥x轴于D,∵A(0,2),B(4,3),
∴OA=2,BD=3,OD=4,
根据题意得:∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴OA:BD=OC:DC=AC:BC=2:3,
∴OC=
| 2 |
| 5 |
| 2 |
| 5 |
| 8 |
| 5 |
∴AC=
| OA2+OC2 |
2
| ||
| 5 |
∴BC=
3
| ||
| 5 |
∴AC+BC=
| 41 |
即这束光从点A到点B所经过的路径的长为:
| 41 |
故答案为:
| 41 |
点评:此题考查了相似三角形的判定与性质、勾股定理以及点与坐标的性质.此题难度适中,解此题的关键是掌握辅助线的作法,掌握入射光线与反射光线的关系.

练习册系列答案
相关题目
 (2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
(2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
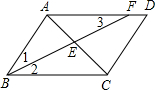 (2012•陕西)如图,在?ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
(2012•陕西)如图,在?ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.