题目内容
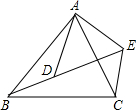如图，已知AB：AD=BC：DE=AC：AE，请猜想∠ABD与∠ACE的关系，并说明理由．
解：∵AB：AD=BC：DE=AC：AE，
∴△ABC∽△ADE．
所以∠BAC=∠DAE，∠BAD=∠CAE，
又AB：AD=AC：AE，∠BAD=∠CAE，
∴△BAD∽△CAE，
∴∠ABD=∠ACE．
分析：由三边对应成比例的两个三角形相似可得△ABC∽△ADE，根据相似三角形的对应角相等得到所以∠BAC=∠DAE，∠BAD=∠CAE，再由两边对应成比例且夹角相等得到△BAD∽△CAE，根据相似三角形的对应角相等即可得出两角的关系．
点评：考查相似三角形的判定定理及性质的应用．
∴△ABC∽△ADE．
所以∠BAC=∠DAE，∠BAD=∠CAE，
又AB：AD=AC：AE，∠BAD=∠CAE，
∴△BAD∽△CAE，
∴∠ABD=∠ACE．
分析：由三边对应成比例的两个三角形相似可得△ABC∽△ADE，根据相似三角形的对应角相等得到所以∠BAC=∠DAE，∠BAD=∠CAE，再由两边对应成比例且夹角相等得到△BAD∽△CAE，根据相似三角形的对应角相等即可得出两角的关系．
点评：考查相似三角形的判定定理及性质的应用．
练习册系列答案
相关题目
