题目内容
 (2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为
(2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为(-1,-1)
(-1,-1)
.分析:连接AD,根据图形得出AD两对应点的坐标,求出其中点坐标即为P点坐标.
解答: 解:连接AD,
解:连接AD,
∵将△ABC绕点P旋转180°得到△DEF,
∴点A旋转后与点D重合,
∵由题意可知A(0,1),D(-2,-3)
∴对应点到旋转中心的距离相等,
∴线段AD的中点坐标即为点P的坐标,
∴点P的坐标为(
,
),即P(-1,-1).
故答案为:(-1,-1).
 解:连接AD,
解:连接AD,∵将△ABC绕点P旋转180°得到△DEF,
∴点A旋转后与点D重合,
∵由题意可知A(0,1),D(-2,-3)
∴对应点到旋转中心的距离相等,
∴线段AD的中点坐标即为点P的坐标,
∴点P的坐标为(
| -2 |
| 2 |
| 1-3 |
| 2 |
故答案为:(-1,-1).
点评:本题考查的是坐标与图形变化-旋转,熟知图形旋转前后的对应点到旋转中心的距离相等是解答此题的关键.

练习册系列答案
相关题目
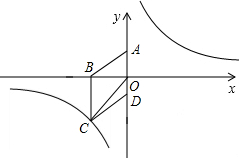 (2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).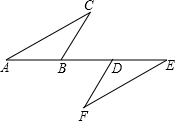 (2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
(2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.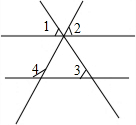 (2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4=
(2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4= (2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=
(2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=