题目内容
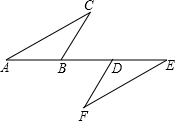 (2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
(2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.分析:根据BC∥DF证得∠CBD=∠FDB,利用利用等角的补角相等证得∠ABC=∠EDF,然后根据AD=EB得到AB=ED,利用AAS证明两三角形全等即可.
解答:证明:∵AD=EB
∴AD-BD=EB-BD,即AB=ED
又∵BC∥DF,
∴∠CBD=∠FDB
∴∠ABC=∠EDF
在△ABC和△EDF中,
∵
∴△ABC≌△EDF,
∴AC=EF
∴AD-BD=EB-BD,即AB=ED
又∵BC∥DF,
∴∠CBD=∠FDB
∴∠ABC=∠EDF
在△ABC和△EDF中,
∵
|
∴△ABC≌△EDF,
∴AC=EF
点评:本题考查了全等三角形的判定与性质,解题的关键是选择最合适的方法证明两三角形全等.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
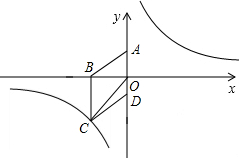 (2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).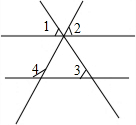 (2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4=
(2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4= (2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为
(2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为 (2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=
(2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=