题目内容
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点（﹣2，0），（x，0），且1＜x1＜2，与y轴的正半轴的交点在（0，2）的下方，下列结论正确的是（ ）
①4a﹣2b+c=0
②a＜b＜0
③2a+c＞0
④2a﹣b+1＞0．
A．①②③ B．②③④ C．①③④ D．①②③④
【答案】D．
【解析】
试题分析：①由函数图象过点（﹣2，0），将点（﹣2，0）代入到抛物线解析式即可得知①正确；②结合函数图象与x轴的交点横坐标可以得知抛物线对称轴﹣
＜﹣
＜0，再由抛物线与y轴的交点在y轴正半轴得知a＜0，解不等式即可得知②正确；③令ax2+bx+c=0，由根与系数的关系即可得出关于
的不等式，解不等式得出c与a之间的关系，将其代入2a+c即可得知③正确；④由抛物线与y轴交点坐标的范围可找出c的范围，结合③中c与a的关系可得出a的取值范围，再结合②结论即可得知④正确．综上即可得出结论．故选D．
练习册系列答案
导学教程高中新课标系列答案
相关题目
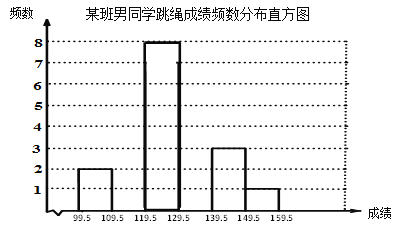
【题目】我校八年级全体男同学参加了跳绳比赛.从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表:
组别 | 99.5﹣109.5 | 109.5﹣119.5 | 119.5﹣129.5 | 129.5﹣139.5 | 139.5﹣149.5 | 149.5﹣159.5 |
频数 | 2 | 4 | 8 | 7 | 3 | 1 |
根据上面统计信息，解答下列问题：
（1）补全频数分布直方图；
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励；
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
