��Ŀ����
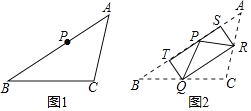
����Ŀ����ͼ1����ͬһƽ���ڣ�������AB��BC��CD��DA��β˳����ӣ�AD��BC�ཻ�ڵ�O��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ���B��������D������

��1����ͼ2��AM��CN�ཻ�ڵ�P��
�ٵ�������ʱ���жϡ�APC�����Ĵ�С��ϵ����˵�����ɣ�
�ڵ�������ʱ����ֱ��д����APC����������������ϵ��
��2���Ƿ����AM��CN������������ڣ����жϲ�˵����������������ϵ���������ڣ���˵�����ɣ�
���𰸡���1���ٵ�������ʱ����APC���������ɼ��������ڵ�������ʱ����APC��![]() ����+������
����+������
��2�������ڣ����ɼ�����.
��������
��1���ٵ���=��ʱ�������������ڽǺͶ����á�2+��D=��4+��APC����OCD+��D=��B+��OAB�����OCD=��OAB�����ݽ�ƽ���߶���á�2=��4�����ԡ�APC=��D=�����ڡ�2+��D=��4+��APC����OCD+��D=��B+��OAB�����2+��=��4+��APC��2��2+��=��+2��4�����ԡ�APC=![]() ����+������
����+������
��2����AM��CN�����4=��5���ɡ�5=��2+��D�õ���4=��2+����ͬ���á�3=��1+����Ȼ�������ʽ��ӵõ���+��=0���ɴ��жϲ�����AM��CN��
��1����ͼ2��
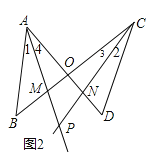
�ٵ�������ʱ����APC�������������£�
����ANP����CND����2+��D����4+��APC��
����AOB����COD����OCD+��D����B+��OAB��
�ߡ�D����B������
���OCD����OAB��
��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�
���OCD��2��2����OAB��2��4��
���2����4��
���APC����D������
�ڵ�������ʱ����APC��![]() ����+������
����+������
�ߡ�2+��D=��4+��APC����OCD+��D=��B+��OAB��
���2+��=��4+��APC��2��2+��=��+2��4��
���APC=��2-��4+������2-��4=![]() ��-
��-![]() ��
��
���APC=![]() ��-
��-![]() ��+��=
��+��=![]() ��+
��+![]() ����
����
���ԡ�APC=![]() ����+������
����+������
��2�������ڣ��������£�
��ͼ1��
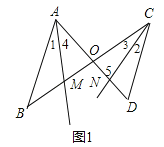
��AM��CN�����4����5��
�ߡ�5����2+��D��
���4����2+����
ͬ���á�3����1+��B������3����1+����
���3+��4����1+��2+��+����
��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�
���3����2����1����4��
����+����0��
�����AM��CN��

 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�����Ŀ����ͥ����ҩƷ����������Σ�շ�����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ���˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������飮
��Ƶ��鷽ʽ��
��1��������ѡȡ�����ķ���
����������ij���������Լ�ͥΪ��λ�����ȡ
����ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ
����ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
�����������һ������ ������ֻ��������ȷ�𰸵���ţ�
�ռ��������ݣ�
���γ������鷢�֣����ܵ���ļ�ͥ���й���ҩƷ���ֽ��й����ݳ������±���
���� ��ʽ | A ����ʹ�� | B ֱ�Ӷ��� | C �ͻ��յ� | D ���ü��� | E ����ҩ�� | F ֱ�ӷ��� |
��ռ���� | 8% | 51% | 10% | 20% | 6% | 5% |
�������ݣ�
��2���˴γ�����������Ϊ1000����ͥ�������������ͳ��ͼ�������ִ�������ҩƷ��ʽ�ļ�ͥ����

�������ݣ�
��3�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��˵��������ɣ�
��4����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������500��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮