题目内容
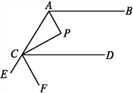
【题目】如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处.
(1)求∠ECF的度数;
(2)若CE=4,B'F=1,求线段BC的长和△ABC的面积.
【答案】(1)∠ECF=45°;(2)BC=![]() ,和△ABC的面积为
,和△ABC的面积为![]() .
.
【解析】
(1)由折叠可得,∠ACE=∠DCE=![]() ∠ACD,∠BCF=∠B'CF=
∠ACD,∠BCF=∠B'CF=![]() ∠BCB',再根据∠ACB=90°,即可得出∠ECF=45°;
∠BCB',再根据∠ACB=90°,即可得出∠ECF=45°;
(2)在Rt△BCE中,根据勾股定理可得BC=![]() ,设AE=x,则AB=x+5,根据勾股定理可得AE2+CE2=AB2﹣BC2,即x2+42=(x+5)2﹣41,求得x=
,设AE=x,则AB=x+5,根据勾股定理可得AE2+CE2=AB2﹣BC2,即x2+42=(x+5)2﹣41,求得x=![]() ,即可得出S△ABC=
,即可得出S△ABC=![]() AB×CE=
AB×CE=![]() .
.
解:(1)由折叠可得,∠ACE=∠DCE=![]() ∠ACD,∠BCF=∠B'CF=
∠ACD,∠BCF=∠B'CF=![]() ∠BCB',
∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=![]() ×90°=45°,
×90°=45°,
即∠ECF=45°;
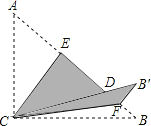
(2)由折叠可得,∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
∴再Rt△BCE中,BC=![]()
设AE=x,则AB=x+5,
∵在Rt△ACE中,AC2=AE2+CE2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AE2+CE2=AB2﹣BC2,
即x2+42=(x+5)2﹣41,
解得x=![]()
∴S△ABC=![]() AB×CE=
AB×CE=![]() (
(![]() +5)×4=
+5)×4=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目