题目内容
(本小题满分8分)
已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2)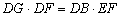 .
.

【答案】
证明:(1)∵AB=AC,∴∠ABC=∠ACB.…………………………………………1分
∵DE∥BC,∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED. …………………………………………1分
∵∠EDF=∠ABE,∴△DEF∽△BDE.…………………………………………1分
(2)由△DEF∽△BDE,得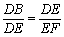 .
.
∴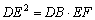 . …………………………………………1分
. …………………………………………1分
由△DEF∽△BDE,得∠BED=∠DFE.
∵∠GDE=∠EDF,∴△GDE∽△EDF.…………………………………1分
∴ . …………………………………………1分
. …………………………………………1分
∴ . …………………………………………1分
. …………………………………………1分
∴ . …………………………………………1分
. …………………………………………1分
【解析】略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 (本小题满分6分,请在下列两个小题中,任选其一完成即可)
(本小题满分6分,请在下列两个小题中,任选其一完成即可)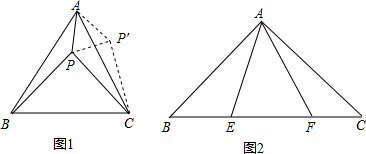
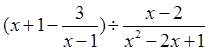
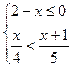 ,并
,并 来.
来.