题目内容
（2011贵州安顺，25，10分）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．
⑴说明四边形ACEF是平行四边形；
⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．
⑴说明四边形ACEF是平行四边形；
⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．
（1）证明：由题意知∠FDC =∠DCA = 90°．∴EF∥CA ∴∠AEF =∠EAC
∵AF = CE =
AE ∴∠F =∠AEF =∠EAC =∠ECA 又∵AE = EA
∴△AEC≌△EAF，∴EF = CA，∴四边形ACEF是平行四边形 ．
（2）当∠B=30°时，四边形ACEF是菱形 ．
理由是：∵∠B=30°，∠ACB=90°，∴AC=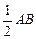
，∵DE垂直平分BC，∴BE=CE
又∵AE=CE，∴CE=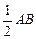，∴AC=CE，∴四边形ACEF是菱形．
∵AF = CE =
AE ∴∠F =∠AEF =∠EAC =∠ECA 又∵AE = EA∴△AEC≌△EAF，∴EF = CA，∴四边形ACEF是平行四边形 ．
（2）当∠B=30°时，四边形ACEF是菱形 ．
理由是：∵∠B=30°，∠ACB=90°，∴AC=
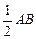，∵DE垂直平分BC，∴BE=CE又∵AE=CE，∴CE=
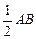，∴AC=CE，∴四边形ACEF是菱形．略
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
C，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连接DE．
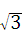，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．
是平行四边形
的对角线
上的点，
，请你猜想：线段
与线段
有怎样的关系？并对你的猜想加以证明。
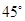，则它的边数是
.
?若存在，请求出该点坐标，若不存在，请说明理由.