ЬтФПФкШн
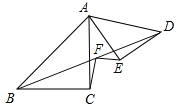
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїABCЃЌЁїADEЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯAED=90ЁуЃЎЃЈ1ЃЉШчЭМ1ЃЌЕуEдкABЩЯЃЌЕуDгыCжиКЯЃЌFЮЊЯпЖЮBDЕФжаЕуЃЎдђЯпЖЮEFгыFCЕФЪ§СПЙиЯЕЪЧ ЃЛЁЯEFDЕФЖШЪ§ЮЊ ЃЛ
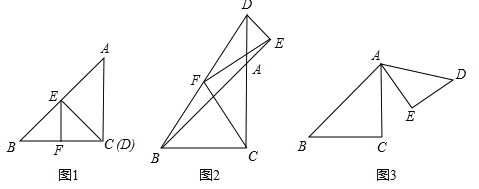
ЃЈ2ЃЉШчЭМ2ЃЌдкЭМ1ЕФЛљДЁЩЯЃЌНЋЁїADEШЦAЕуЫГЪБеыа§зЊЕНШчЭМ2ЕФЮЛжУЃЌЦфжаDЁЂAЁЂCдквЛЬѕжБЯпЩЯЃЌFЮЊЯпЖЮBDЕФжаЕуЃЎдђЯпЖЮEFгыFCЪЧЗёДцдкФГжжШЗЖЈЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉШєЁїADEШЦAЕуШЮвта§зЊвЛИіНЧЖШЕНШчЭМЂлЕФЮЛжУЃЌFЮЊЯпЖЮBDЕФжаЕуЃЌСЌНгEFЁЂFCЃЌЧыФуЭъГЩЭМ3ЃЌЧыВТЯыЯпЖЮEFгыFCЕФЙиЯЕЃЌВЂбщжЄФуЕФВТЯы.
ЁОД№АИЁПЃЈ1ЃЉEF=FCЃЌ90ЁуЃЎЃЈ2ЃЉEF=FCЃЌEFЁЭFCЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉEF=FCЃЌEFЁЭFC.
ЁОНтЮіЁП
ЪдЬтНтЮіЃКЃЈ1ЃЉвзЕУЁїEFCЪЧЕШбќжБНЧШ§НЧаЮЃЌФЧУДEF=FCЃЌЁЯEFD=90ЁуЃЎ
ЃЈ2ЃЉбгГЄЯпЖЮCFЕНMЃЌЪЙЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂECЃЌвзжЄЁїBFCЁеЁїDFMЃЌНјЖјПЩвджЄУїЁїMDEЁеЁїCAEЃЌМДПЩжЄУїEF=FCЃЌEFЁЭFCЃЛ
ЃЈ3ЃЉЛљБОЗНЗЈЭЌЃЈ2ЃЉЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉEF=FCЃЌ90ЁуЃЎ
ЃЈ2ЃЉбгГЄCFЕНMЃЌЪЙЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂEC
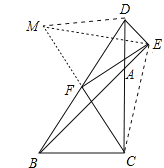
ЁпFC=FMЃЌЁЯBFC=ЁЯDFMЃЌDF=FBЃЌ
ЁрЁїBFCЁеЁїDFMЃЌ
ЁрDM=BCЃЌЁЯMDB=ЁЯFBCЃЌ
ЁрMD=ACЃЌMDЁЮBCЃЌ
ЁпED=EAЃЌЁЯMDE=ЁЯEAC=135ЁуЃЌ
ЁрЁїMDEЁеЁїCAEЃЌ
ЁрME=ECЃЌЁЯDEM=ЁЯCEAЃЌ
ЁрЁЯMEC=90ЁуЃЌ
ЁрEF=FCЃЌEFЁЭFC
ЃЈ3ЃЉEF=FCЃЌEFЁЭFCЃЎ