题目内容
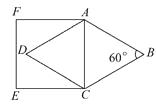
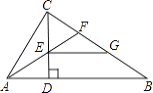
【题目】如图,等边△ABC的面积为S ,⊙O是它的外接圆,点P是弧BC的中点.(1)试判断过点C所作⊙O的切线与直线AB是否相交,并证明你的结论.(2)设直线CP与AB相交于点D,过点B作BE⊥CD,垂足为E,证明BE是⊙O的切线,并求△BDE的面积.

【答案】(1) CF是⊙O的切线CF与直线AB不相交. (2) ![]() S
S
【解析】试题分析:(1)作⊙O的切线CF,判断出∠BCF=∠ABC,得到CF∥AB,可知CF与直线AB不相交.
(2)OB是圆O直径,证出∠HBE=90°,可得BE是⊙O的切线,并将S△BDE转化为S△BCE.
试题解析:
(1)CF是⊙O的切线CF与直线AB不相交.
证明如下:
CF是⊙O的切线,△ABC是等边三角形,
![]()
![]()
![]() CF∥AB.
CF∥AB.
![]() CF与直线AB不相交;
CF与直线AB不相交;
(2)连结BO并延长交AC于H.
![]() ⊙O是等边△ABC的外接圆,
⊙O是等边△ABC的外接圆,
![]()
![]() 点P是BC的中点,
点P是BC的中点,
![]() .
.
又![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() BE是⊙O的切线.在△ACD中,
BE是⊙O的切线.在△ACD中,
![]()
![]()
![]()
![]()
![]() S△BDE = S△BCE.在矩形BHCE中,
S△BDE = S△BCE.在矩形BHCE中,
S△BCE =S△BCH = ![]() S
S
![]() S△BCE=
S△BCE=![]() S
S
![]() S△BDE=
S△BDE=![]() S
S


练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目