题目内容
【题目】问题原型:如图①,在锐角![]() 中,
中,![]() ,AD⊥BC于D,在AD上取点E,使
,AD⊥BC于D,在AD上取点E,使![]() ,连结BE.求证:
,连结BE.求证:![]() .问题拓展:如图②,在问题原型的条件下,
.问题拓展:如图②,在问题原型的条件下,![]() 为
为![]() 的中点,连结
的中点,连结![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连结
,连结![]() .
.
图① 图②
图②
(1)判断线段![]() 与
与![]() 的大小关系,并说明理由.(2)若
的大小关系,并说明理由.(2)若![]() ,直接写出
,直接写出![]() 、
、![]() 两点之间的距离.
两点之间的距离.
【答案】问题原型:见解析;(1)![]() ,见解析;(2)
,见解析;(2)![]() .
.
【解析】
问题原型:由AD⊥BC可得∠ADB=∠ADC=90°,又∠ABC=45°可得∠ABC=∠BAD,可得AD=BD,根据SAS定理可得△BDE≌△ADC;
问题拓展:(1)利用SAS判断出△BEF≌△CMF,得出BE=CM,即可得出结论;
(2)借助问题原型与问题延伸的结论判断出△ACM是等腰直角三角形,即可得出结论.
解:问题原型:∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ;
;
问题拓展:(1)![]() .
.
理由:∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ;
;
(2)如图②,
图②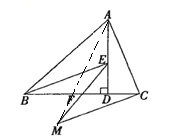
连接AM,由(1)知,△BDE≌△ADC,
∴∠BED=∠ACD,
由(2)知,△BEF≌△CMF,
∴∠EBF=∠BCM,
∴∠ACM=∠ACD+∠BCM=∠BED+∠EBF=90°,
∵AC=CM,
∴AM=![]() AC=4
AC=4![]() .
.
故答案为:(1)![]() ,见解析;(2)
,见解析;(2)![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根据以上信息,解答下列问题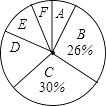
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.