题目内容
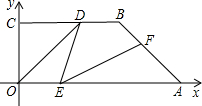
如图.直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上.OA∥BC,OA=4 ,OC=
,OC=
 ,
,
∠OAB=45°,D是BC上一点,CD=
 .E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,设OE=x,AF=y.
.E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,设OE=x,AF=y.
(1)AB=________,BC=________,∠DOE=________;
(2)证明△ODE∽△AEF,并确定y与x之间的函数关系;
(3)当AF=EF时,将△AEF沿EF折叠,得到△A′EF,求△A′EF与五边形OEFBC重叠部分的面积.
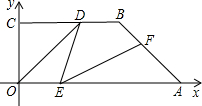
 解:(1)过B作BM⊥OA于M,
解:(1)过B作BM⊥OA于M,则四边形CBMO是矩形,
∵∠BAO=45°,
∴BC=OM,OC=BM=MA=

 ,
,由勾股定理得:AB=
 =3,
=3,BC=OA-AM=
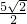 ,
,∵CD=OC,
∴∠COD=∠CDO=45°,
∴∠DOE=45°,
故答案为:3,
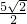 ,45°.
,45°.(2)证明:∵∠BAO=∠DOE=45°,
∵∠ODE=∠DEA-45°,∠FEA=∠DEA-45°,
∴∠ODE=∠FEA,
∴△ODE∽△AEF,
∴
 =
= ,
,即
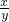 =
=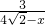 ,
,∴y=-
 x2+
x2+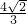 x,
x,即y与x的函数关系式是y=-
 x2+
x2+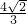 x.
x.(3)
 当EF=AF时,如图,∠FAE=∠FEA=∠DEF=45°,
当EF=AF时,如图,∠FAE=∠FEA=∠DEF=45°,∴△AEF是等腰直角三角形,D在A'E上,A'E⊥OA,B在A'F上,A'F⊥EF,
∴△A'EF与五边形OEBC重叠部分的面积为四边形EFBD的面积,
∵AE=OA-OE=OA-CD=4
 -
-
 =
=
 ,
,∴AF=EF=

 ÷
÷ =
= ,
,∴S△AEF=
 EF•AF=
EF•AF= ×
× =
=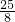 ,
,∴S梯形AEDB=
 (BD+AE)•DE=
(BD+AE)•DE= ×(
×( +
+
 )×
)×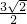 =
=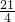 ,
,∴S四边形BDEF=S梯形AEDB-S△AEF=
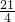 -
-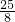 =
=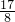 .
.分析:(1)过B作BM⊥OA于M,证四边形CBMO是矩形,推出CB=OM,OC=BM=AM,即可求出答案;
(2)证△ODE∽△AEF,根据相似三角形的性质得到比例式,即可求出答案;
(3)若AF=EF,此时△AEF是等腰Rt△,A′在AB的延长线上,重合部分是四边形EDBF,其面积可由梯形ABDE与△AEF的面积差求得.
点评:本题主要考查对直角梯形,相似三角形的性质和判定,矩形的性质和判定,三角形的面积,坐标与图形性质,翻折变换等知识点的理解和掌握,能综合运用这些性质进行计算和推理是解此题的关键.

练习册系列答案
相关题目
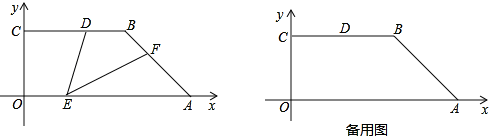
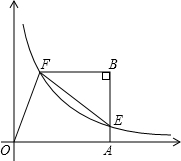 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=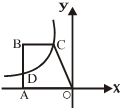 如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=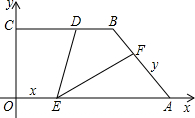 是BC上一点,BD=
是BC上一点,BD=