题目内容
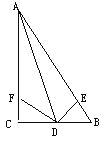
【题目】已知△ABC,D、E分别为AC、AB中点,BD和CE交于点O,BD和CE是一元二次方程x2﹣kx+24=0的两个不等实根,则△BOE面积的最大值为( )
A.![]()
B.2
C.![]()
D.4
【答案】C
【解析】解:∵D、E分别为AC、AB中点,BD和CE交于点O,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
∴△DOE∽△BOC,
∴OD:OB=OE:OC=DE:BC=1:2,
∴OE= ![]() CE,OB=
CE,OB= ![]() BD,
BD,
∵BD和CE是一元二次方程x2﹣kx+24=0的两个不等实根,
∴BDCE=24,
若△BOE面积最大,则△BOE是直角三角形,
分两种情况:
①若∠BEO=90°,则CE⊥AB,
∵E是AB的中点,
∴AC=BC,
同理:AB=BC,
则△ABC是等边三角形,
∴BD=CE,不合题意;
②当∠BOE=90°时,△BOE的面积= ![]() OEOB=
OEOB= ![]() ×
× ![]() CE×
CE× ![]() BD=
BD= ![]() ×
× ![]() ×
× ![]() ×24=
×24= ![]() ;
;
故选:C.
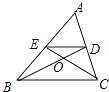
【考点精析】根据题目的已知条件,利用根与系数的关系和三角形中位线定理的相关知识可以得到问题的答案,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目