题目内容
 如图,四边形ABDC中,AD平分∠BAC,DB=DC,
如图,四边形ABDC中,AD平分∠BAC,DB=DC,
(1)判断点D到AB与AC的距离关系?并用一句话叙述理由;
(2)试说明△ABC是等腰三角形.
 解:(1)点D到AB与AC的距离相等.
解:(1)点D到AB与AC的距离相等.理由如下:角平分线上的点到角两边的距离相等.
(2)作DM⊥AB交AB延长线于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,
∴DM=DN,
∵DB=DC,
∴Rt△BMD≌Rt△NDC(HL),
∴BM=CN,
∵AD=AD,DM=DN,
∴△AMD≌△AND(HL),
∴AM=AN,
∴AB=AC.
分析:(1)点D到AB与AC的距离相等.理由是角平分线上的点到角两边的距离相等.
(2)作DM⊥AB交AB延长线于M,DN⊥AC交AC延长线于N,根据角平分线的性质可证DM=DN,根据HL可证出Rt△BMD≌Rt△NDC,得BM=CN,根据HL再证出△AMD≌△AND得AM=AN,即证AB=AC.
点评:本题重点考查了三角形全等的判定及性质、等腰三角形的判定;普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等.注意角平分线的性质运用非常广泛.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
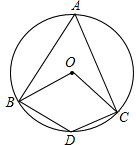 如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )
如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )| A、60° | B、120° | C、80° | D、100° |
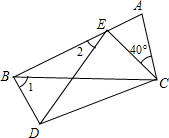 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=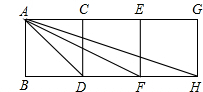 如图,四边形ABDC、CDFE、EFHG都是正方形.
如图,四边形ABDC、CDFE、EFHG都是正方形.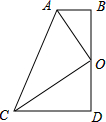 如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.
如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.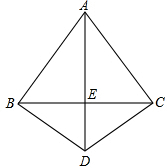 如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.
如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.