题目内容
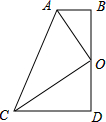 如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.
如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
分析:(1)过点O作OE⊥AC于E,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;
(2)利用“HL”证明△ABO和△AEO全等,根据全等三角形对应角相等可得∠AOB=∠AOE,同理求出∠COD=∠COE,然后求出∠AOC=90°,再根据垂直的定义即可证明;
(3)根据全等三角形对应边相等可得AB=AE,CD=CE,然后证明即可.
(2)利用“HL”证明△ABO和△AEO全等,根据全等三角形对应角相等可得∠AOB=∠AOE,同理求出∠COD=∠COE,然后求出∠AOC=90°,再根据垂直的定义即可证明;
(3)根据全等三角形对应边相等可得AB=AE,CD=CE,然后证明即可.
解答:证明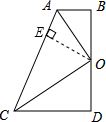 :(1)过点O作OE⊥AC于E,
:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=
×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
 :(1)过点O作OE⊥AC于E,
:(1)过点O作OE⊥AC于E,∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
|
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=
| 1 |
| 2 |
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,到角的两边距离相等的点在角的平分线上,以及全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
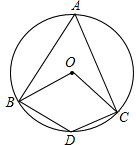 如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )
如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )| A、60° | B、120° | C、80° | D、100° |
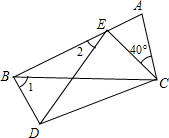 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=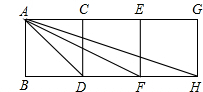 如图,四边形ABDC、CDFE、EFHG都是正方形.
如图,四边形ABDC、CDFE、EFHG都是正方形.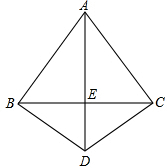 如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.
如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.