题目内容
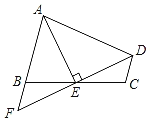
【题目】某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
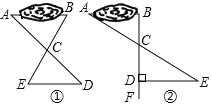
方案1:如图(1),先在平地上取一个可以直接到达A、B的点C,连接AC并延长AC至点D,连接BC并延长至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长.
方案2:如图(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB间的距离
问:(1)方案1是否可行?并说明理由;
(2)方案2是否可行?并说明理由;
(3)小明说:“在方案2中,并不一定需要BF⊥AB,DE⊥BF,将“BF⊥AB,DE⊥BF”换成条 也可以.”你认为小明的说法正确吗?如果正确的话,请你把小明所说的条件补上.
【答案】(1)可行,理由见解析;(2)可行,理由见解析;(3)AB∥DE
【解析】
(1)利用SAS定理证明△ABC≌△DEC可得AB=DE;
(2)利用ASA定理证明△ABC≌△DEC可得AB=DE;
(3)AB∥DE,可得∠B=∠BDE,利用ASA定理证明△ABC≌△DEC可得AB=DE.
解:(1)在△ABC和△DEC中,
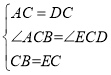 ,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)∵BF⊥AB,DE⊥BF,
∴∠B=∠BDE,
在△ABC和△DEC中,
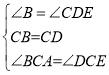 ,
,
∴△ABC≌△DEC(ASA),
∴AB=DE;
(3)只需AB∥DE即可,
∵AB∥DE,
∴∠B=∠BDE,
在△ABC和△DEC中,
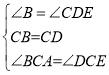 ,
,
∴△ABC≌△DEC(ASA),
∴AB=DE,
故答案为:AB∥DE.

 阅读快车系列答案
阅读快车系列答案【题目】一根弹簧的长度为10厘米,当弹簧受到![]() 千克的拉力时(
千克的拉力时(![]() 不超过10),弹簧的长度是
不超过10),弹簧的长度是![]() (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:
拉力 | 1 | 2 | 3 | 4 | … |
弹簧的长度 |
|
|
|
| … |
(1)写出弹簧长度![]() (厘米)关于拉力
(厘米)关于拉力![]() (千克)的函数解析式;
(千克)的函数解析式;
(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?