题目内容
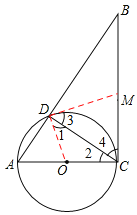
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.

【答案】(1)证明见解析;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切,理由见解析.
【解析】
试题分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;
(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.
试题解析:(1)证明:∵AC为直径,∴∠ADC=90°. ∴∠A+∠DCA=90°.
∵∠ACB=90°,∴∠DCB+∠ACD=90°. ∴∠DCB=∠A.
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切,理由如下:
如答图,连接DO,
∵DO=CO,∴∠1=∠2.
∵DM=CM,∴∠4=∠3.
∵∠2+∠4=90°,∴∠1+∠3=90°. ∴直线DM与⊙O相切.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )
阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
A.中位数是2
B.平均数是2
C.众数是2
D.极差是2

