题目内容
已知如图，有一块三角板DEF（∠D=90°）放置在△ABC上，恰好三角板DEF的两条直角边DE、DF分别经过点B、C，△ABC中，∠A=30°，改变直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过B、C，那么∠ABD+∠ACD=________．
60°
分析：本题考查的是三角形内角和定理．已知∠A=30°易求∠ABC+∠ACB的度数．又因为∠D为90°，所以易求∠DBC+∠DCB，相减即可求出∠ABD+∠ACD．
解答：∵∠A=30°，
∴∠ABC+∠ACB=150°，
∵∠D=90°，
∴∠DBC+∠DCB=90°，
∴∠DBA+∠DCA=150°-90°=60°．
故答案为：60°．
点评：考查了三角形内角和定理，此题注意运用整体法计算．关键是求出∠ABC+∠ACB．
分析：本题考查的是三角形内角和定理．已知∠A=30°易求∠ABC+∠ACB的度数．又因为∠D为90°，所以易求∠DBC+∠DCB，相减即可求出∠ABD+∠ACD．
解答：∵∠A=30°，
∴∠ABC+∠ACB=150°，
∵∠D=90°，
∴∠DBC+∠DCB=90°，
∴∠DBA+∠DCA=150°-90°=60°．
故答案为：60°．
点评：考查了三角形内角和定理，此题注意运用整体法计算．关键是求出∠ABC+∠ACB．
练习册系列答案
相关题目
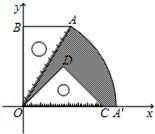已知：如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，
已知如图，有一块三角板DEF（∠D=90°）放置在△ABC上，恰好三角板DEF的两条直角边DE、DF分别经过点B、C，△ABC中，∠A=30°，改变直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过B、C，那么∠ABD+∠ACD=